この記事では、正負の数の加法と減法について解説していきます。
絶対値とか、数直線とかそういう用語はなしにして、
計算のイメージを掴んでもらうための記事です。
この記事を見る前に、正負の数ってどういうものかを解説した記事があります。
まずはそちらを見ることをお勧めします。
正負の数ではこのような計算します。
- (+2)+(+1)=+3
- (+2)-(+1)=+1
- (+2)+(-1)=+1
- (+2)-(-1)=+3
小学校までの算数とちょっと見た目が違います。
+と-が数字の前についたりしていますね。
難しく見えるかもしれませんが、
そこまで難しいルールではありません。
符号と( )
まずは計算の表記について、まず解説します。
プラスとマイナスの符号
0より大きい数を正の数、0より小さい数を負の数と言います。
正の数を表すときには、+(プラス)をつけ、
負の数を表すときには、-(マイナス)をつけます。
この+や-の記号を「符号」と言い、それぞれ正の符号、負の符号と呼びます。
正の数ならば、+1、+15、+3.5
負の数ならば、-1、-15、-3.5のように書きます。
正の数だと区別できるとき、+の符号を省力することが多いです。
+1、+15、+3.5 → 1、15、3.5
-の符号は書かないと区別ができないので絶対に書きます。
+と区別できないのでダメ
-1、-15、-3.5 → 1、15、3.5 にはできない
( )のついた計算
正負の数では、符号が連続する時に( )をつけなければなりません。
(+2)+(+1)=+3
それ以外で付いている場合は、丁寧に表現しているときです。
たとえば、この式の(+2)は( )が無くても問題ありません。
あえてつけることで、後ろの(+1)と表現を合わせています。
( )の省略
+の符号の省略を使うことで、( )も省略することがあります。
( )の中のプラスの数は区別がつくので、+を省略できます。
すると、符号が連続しなくなるので( )を省略できます。
元の式 → +の省略 → ( )の省略
(+2)+(+1)=+3 → (2)+(1)=3 → 2+1=3
(+2)-(+1)=+1 → (2)-(1)=3 → 2-1=3
(+2)+(-1)=+1 → (2)+(-1)=1 → 2+(-1)=1
(+2)-(-1)=+3 → (2)-(-1)=+3 → 2-(-1)=3
符号の連続する時に( )が付く、と思ってください。
正負の数 加法と減法
正負の数の計算について解説していきます。
加法と減法とは、要は足し算と引き算です。
前回の記事同様、重りと風船の例で考えます。
0より小さい数とは、0より大きい数と反対の働きをするものです。
下向きの力をプラスとした時、上向の力をマイナスとすることができます。
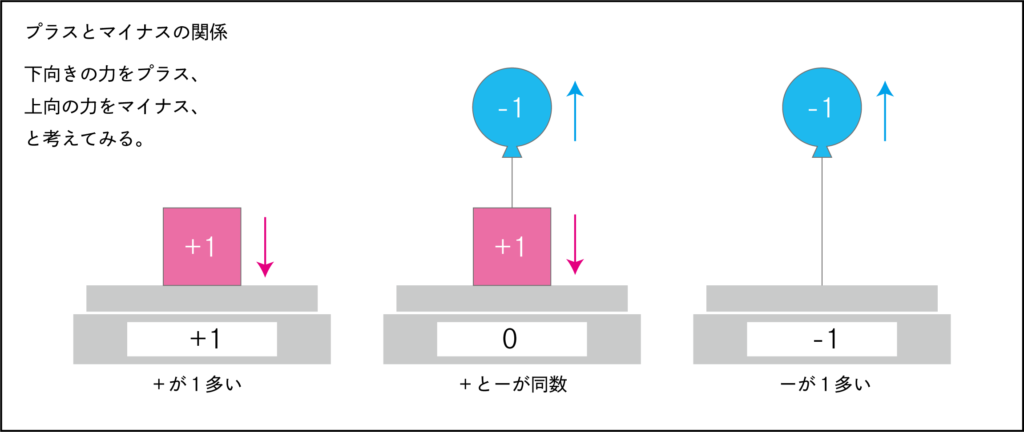
二つの要素の足し算、引き算なので、
次の図のような4パターンが考えられます。
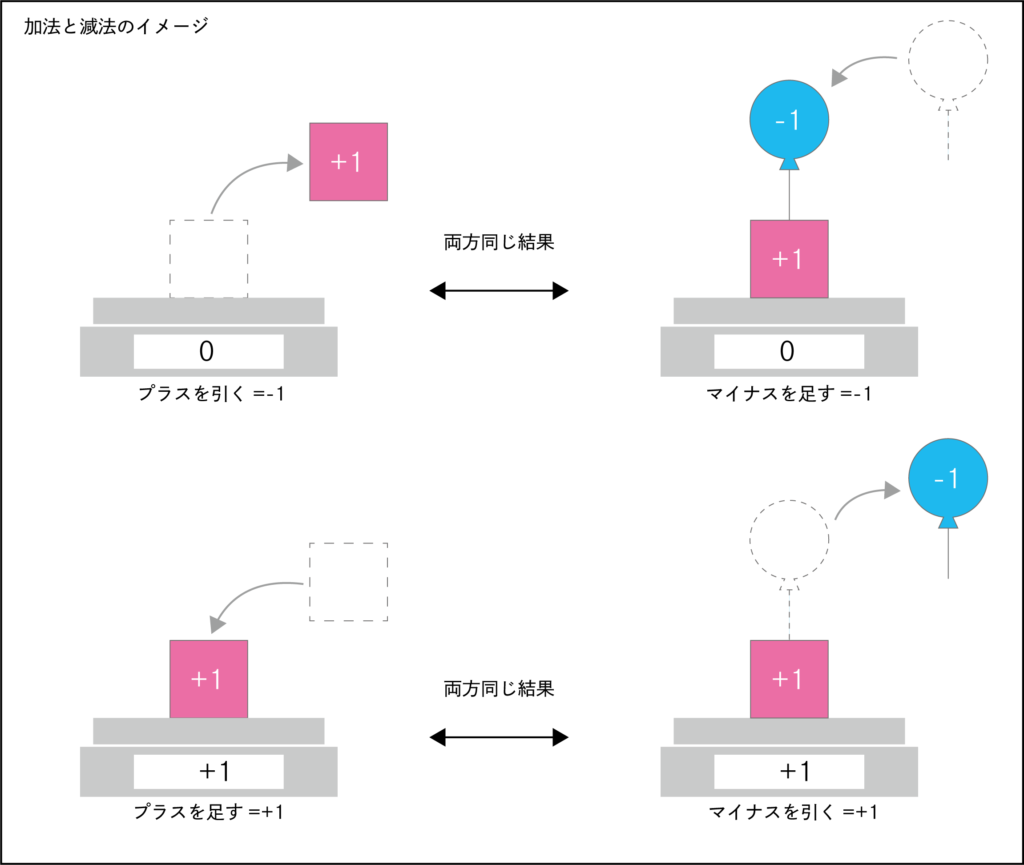
「プラスを引く」と「マイナスを足す」は同じ結果、
「プラスを足す」と「マイナスを引く」は同じ結果、
この4つの操作によって、「増える」と「減る」の二つの結果が得られます。
上の図の場合であれば、
「重りを引く」か「風船を足す」と軽くなり(マイナス)、
「重りを足す」か「風船を引く」と重くなる(プラス)、
ということです。
「プラス」と「マイナス」の要素を足したり、引いたりして、
どちらがどれだけ多いかを計算するのが正負の数です。
計算イメージ
先ほどの4つの計算について考えてみましょう。
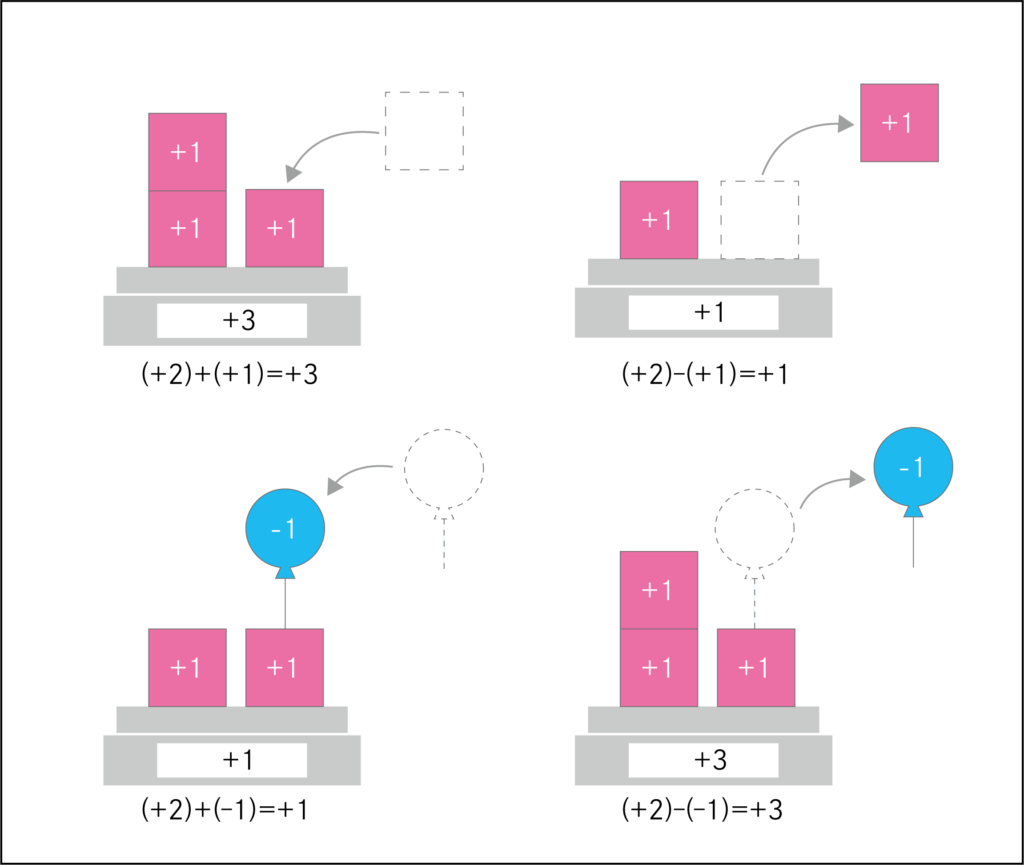
それぞれの計算をイメージに直してみると、このようになります。
(+2)-(-1)=+3が少し分かりづらいかもしれません。
左のように+とーの組み合わせは0なので全体は(+2)、
そこから(-1)を引いて(+3)になります。
計算式は書き換えができる

この図で示すとおり、正負の数の計算では、
操作が違っても同じ結果が得られます。
ですので、計算を書き換えることもできます。
(+2)-(-1)=+3 → (+2)+(+1)=+3
(+2)+(-1)=+1 → (+2)-(+1)=+1
この逆も同様に可能です。
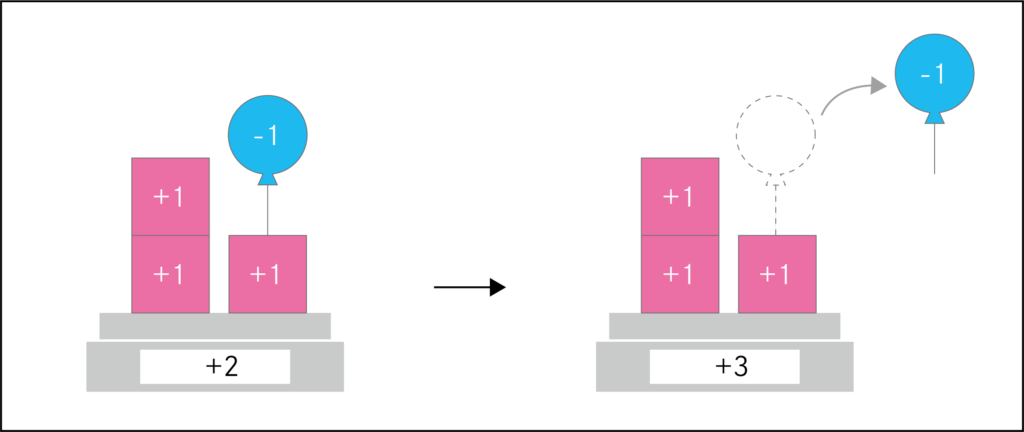
(+2)-(-1)=+3 → (+2)+(+1)=+3
を図で表すと以下のような感じでしょうか。
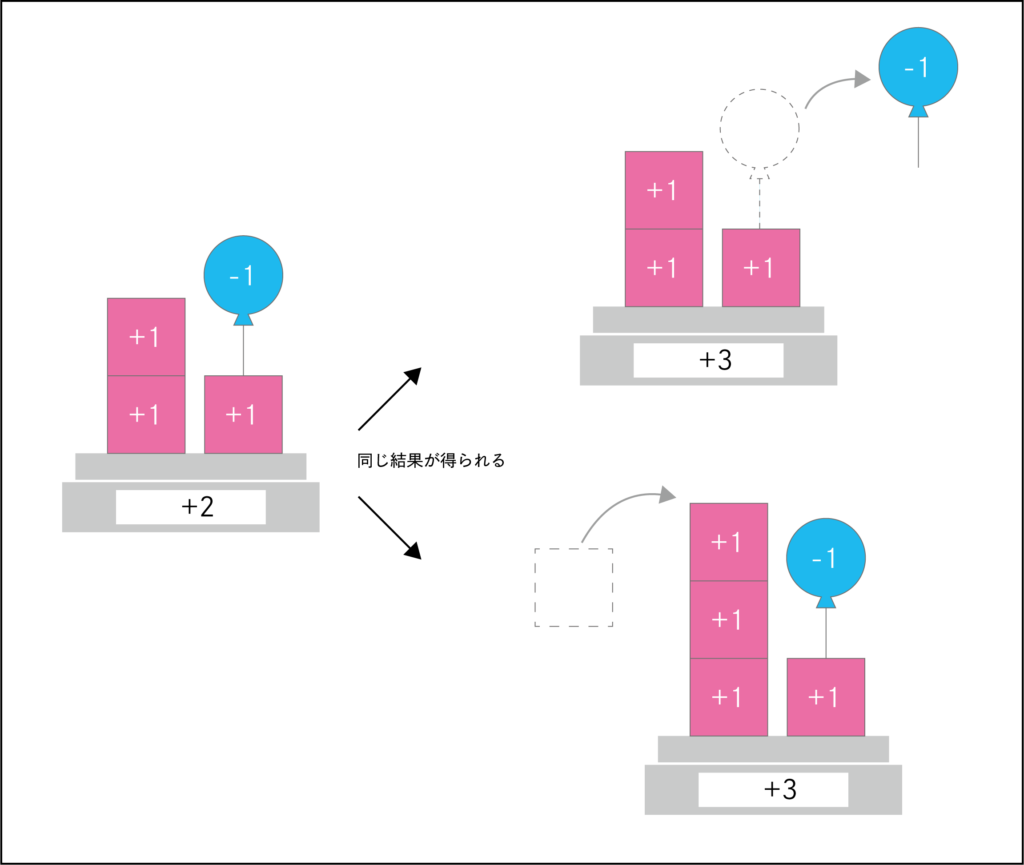
結果が変わらなければ、
「風船を引く」か、「重りを足すか」は計算上区別しません。
もちろん、「風船を足す」か、「重りを引く」かも区別しません。
どちらで計算しても良いということです。
また、書き換えた後、+と( )の省略が可能です。
(+2)-(-1)=+3 → (+2)+(+1)=+3 → 2+1=3
(+2)+(-1)=+1 → (+2)-(+1)=+1 → 2-1=1
計算しやすい式の形に変えるのが良いでしょう。
どの式を状態を使っても大丈夫です。
実際に計算してみよう
実際に問題をいくつか解いてみましょう。
式の下にプラスを●、マイナスを○として表現しています。
●を重り、○を風船のようなものだと考えてください。
●と○のどちらがどれだけ多いかを考えるように計算してみましょう。
●が2個多かったら+2、○が3個多かったら-3のように考えれば大丈夫です。
(+3)+(+5)
●●●+●●●●●
●が8個、○が0個
●が8個多いので+8
(-3)+(-5)
○○○+○○○○○
●が0個、○が8個
○が8個多いので-8
(+3)+(-1)=2
●●●+○
●が3個、○が1個
●が2個多いので+2
(+1)+(-3)=-2
●+○○○
●が1個、○が3個
○が2個多いので-2
(+4)-(+2)
(+4)-(+2)は、(+4)+(-2)と同じなので
●●●●+○○
●が4個、○が2個
●が2個多いので+2
(+2)-(+4)
(+2)-(+4)は、(+2)+(-4)と同じなので
●●+○○○○
●が2個、○が4個
○が2個多いので-2
(-2)-(-4)
(-2)-(-4)は、(-2)+(+4)と同じなので
○○+●●●●
●が4個、○が2個
●が2個多いので+2
これらの考え方は、
教科書に載っている絶対値というものを使った計算と同じです。
まとめ
正負の数の加法と減法の考え方は基本これだけです。
ちょっと頭を使うかもしれませんが、
多少想像がつくようになったのではないでしょうか。
計算規則や長めの問題になると混乱するかもしれません。
しかし、焦らず丁寧取り組めばそこまで難しくないと思います。


コメント