マイナス×マイナスがプラスになる理由を図解します！

なぜマイナス×マイナスがプラスになるのか、なんて答えますか？
正負の数の計算はそこまで難しくないものの、
この部分だけ納得できないということが結構あるのではないかと思います。

この記事ではマイナス×マイナスがプラスになる理由を解説します。

前提知識

マイナス×マイナスがプラスになることが分かるためには、
いくつか前提知識が必要です。

それは

• 0より小さい数と0
• 正負の数の足し算・引き算
• 掛け算とは何か

の3つです。

「0より小さい数」と「0」

さて、「0より小さい数」とはなんでしょう。

次の図を見てください。

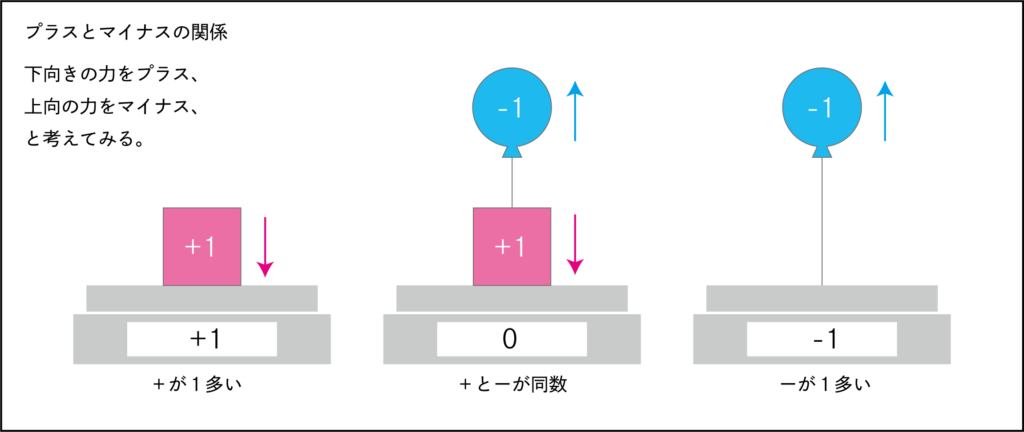
「0より小さい数」というのは図の「風船」みたいなものです。

下向きの力、つまり重さを「プラス」とするのであれば、
上向きの力、その逆の力を「マイナス」として扱います。

また、中央の「重り」と「風船」が一緒になると、
それぞれ打ち消し合い0になります。
物が無くならなくても0になるということです。

正負の数の足し算・引き算

正負の数の足し算・引き算についても見ていきましょう。

正負の数の計算では
「プラス」と「マイナス」のどちらが、どれだけ多いかを数えます。

「プラス」の方が1多かったら+1、
「マイナス」の方が1多かったら-1、
このように考えます。

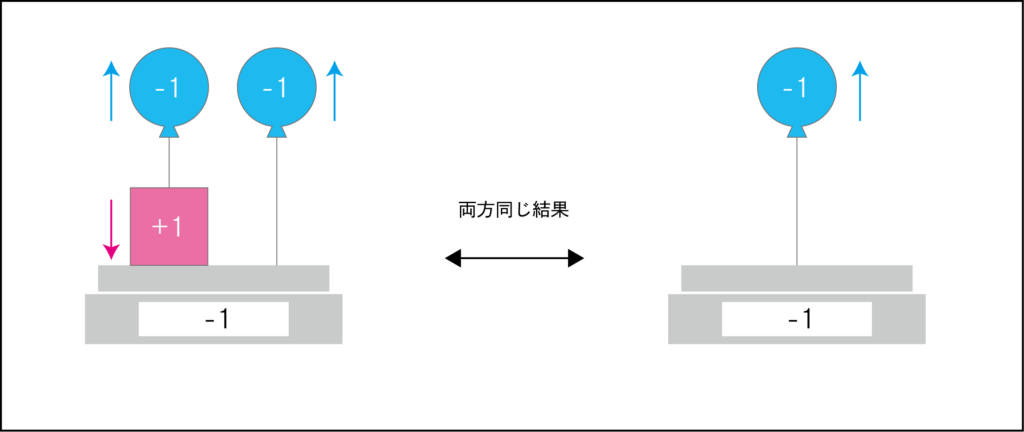
例えば、この図で見ると、
左側はプラスが1個、マイナスが2個なので-1。
右側はプラスが0個、マイナスが2個なので-1。

このように考えます。

4つの計算パターンと書き換え

正負の数の足し算・引き算の計算過程は
以下の図のような4パターンが考えられます。

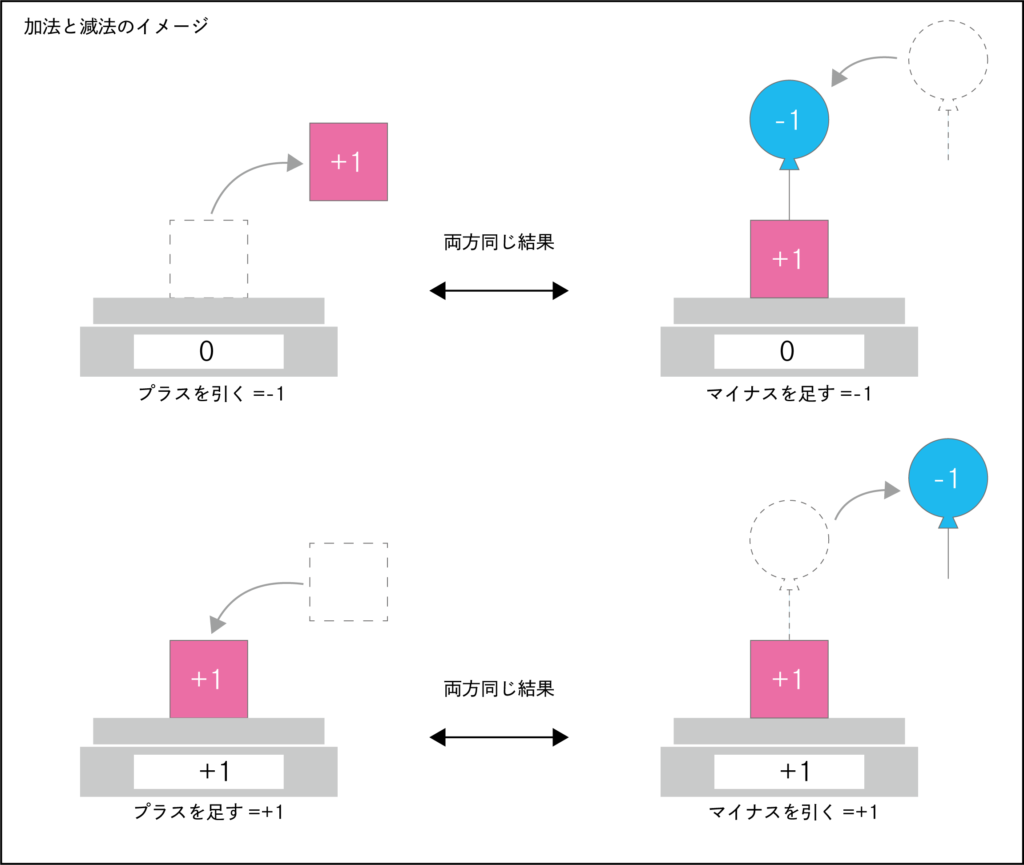
この時、
「プラスを足す」と「マイナスを引く」はプラスの結果、
「プラスを引く」と「マイナスを足す」はマイナスの結果、
それぞれ同じ結果が得られます。

このような、
同じ結果が得られる時、計算式の書き換えが可能になります。

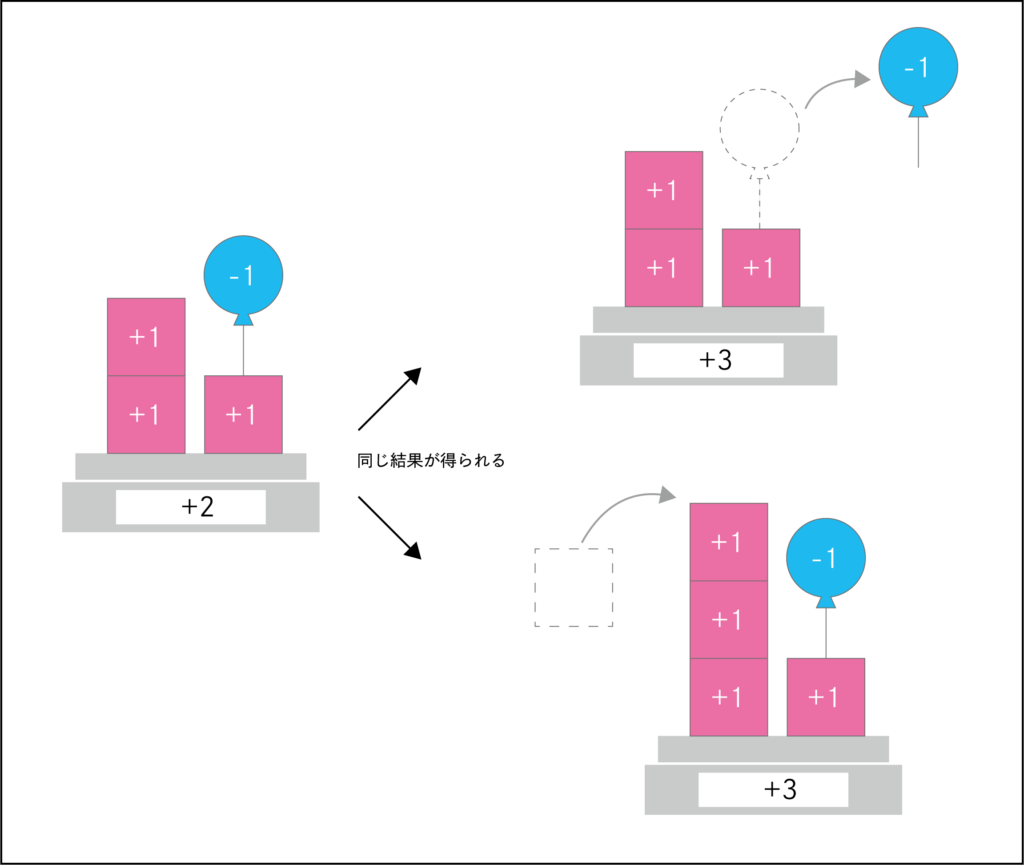
たとえば、+2から+3に増える時、
「重りを足す」と「風船を引く」
のどちらで考えても計算できます。

よって、
\((+2)-(-1)=+3\) を \((+2)-(-1)=+3\)
と書き換えることができます。

「どちらがどれだけ多いか」という差を求める計算だからこそ、
「プラスを足す」と「マイナスを引く」を書き換えても問題ないのです。

掛け算とは何か

さて、掛け算とはどのような計算なのでしょう。
結論を言えば、小学校までの掛け算は足し算の応用です。

例えば、
\((+1)\times(+2)\) なら「1を2回足す」と考えます。
計算式で表すと、\(0+(+1)+(+1)=+2\) です。

では、\((+1)\times(-2)\)はどう考えればよいでしょう。

この計算は引き算の応用として考えてみましょう。

\((+1)\times(-2)\) は「1を2回引く」と考えます。
すると、\(0-1-1=-2\)と計算できます。

同様に、\((-1)\times(-2)\)は「-1を2回引く」ので
\(0-(-1)-(-1)=+2\)と表現することができます。

マイナス×マイナス=プラス

さて、本題に入りましょう。
先ほどまでの話を整理してみます。

この3つを合わせて考えると、
-1×(-2)は「1を2回足す」と考えられる、
ということです。

理屈は分かるかと思いますが、
想像しづらいと思うので図にしてみましょう。

パターン1

\((-1)\times(-2)\)を「-1を2回引く」とし、
(0-(-1)-(-1)=+2)と表現しました。

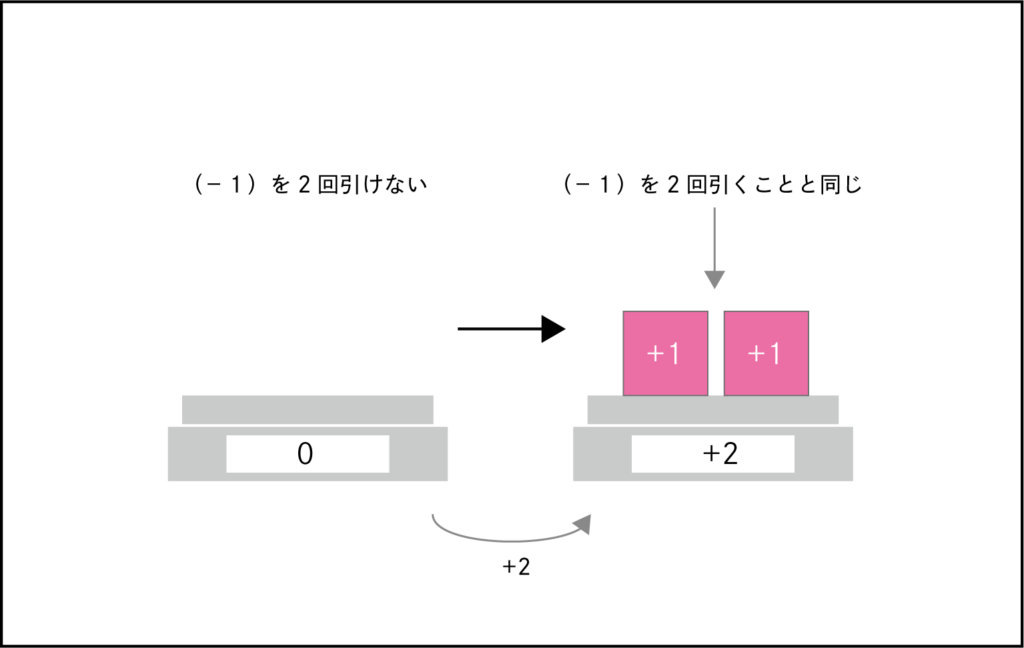
0を「何もない状態」と考えるなら、
「風船」、つまり「マイナス」を引くことができないので、
代わりに、「重りを足す」わけです。

すると、全体の重さが+2となりました。

パターン2

0を「プラス」と「マイナス」が同数の状態と考えると、
「風船」を引くことができます。

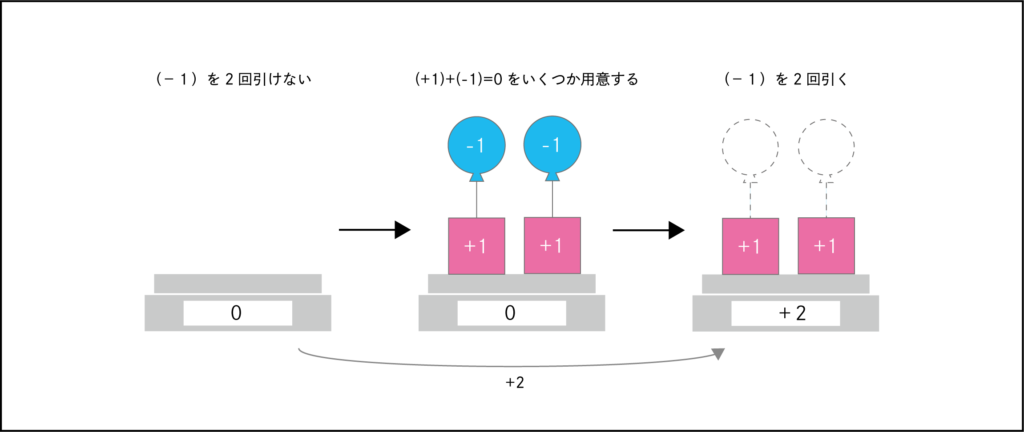
(+1)と(-1)のセットを0と考えます。
0にはいくら０を足しても、答えは0です。

「重り」と「風船」のセットから、
「風船」を引くと「重り」が残ります。

すると、全体の重さが+2となりました。

まとめ

自分が正負の数を習った時、
計算はできるけど、納得しづらいなと思いながら、
勉強した記憶があります。

今も昔も数直線のような無機質なものだと
納得感が少ないのではないでしょうか。
そんな人向けに記事を書いてみました。

今回の解説というのは、
あくまでイメージしやすくするためのものです。

「重り」と「風船」は分かりやすい例えだと感じていますが、
細かい設定などは省いています。

一つの思考実験だとでも考えてください。
他にもいろいろな考え方があると思います。

ただ、数学は様々な解釈が可能なので、
是非いろいろな視点で捉えなおしてみると面白いです。