前編
- \(y=2x+1\) について、xの変域 が 5≦x≦7 のときの yの変域 を求めよ。
- \(y=5x+3\) について、xの変域 が -1≦x≦4 のときの yの変域 を求めよ。
- \(y=-3x+2\) について、xの変域 が 2≦x≦5 のときの yの変域 を求めよ。
- \(y=-2x-5\) について、xの変域 が -5≦x≦-2 のときの yの変域 を求めよ。
- \(y=8x+3\) について、xの変域 が 1≦x のときの yの変域 を求めよ。
- \(y=8x+3\) について、xの変域 が x≦1 のときの yの変域 を求めよ。
- \(y=-2x+4\) について、xの変域 が 3≦x のときの yの変域 を求めよ。
- \(y=-2x+4\) について、xの変域 が x≦-2 のときの yの変域 を求めよ。
後編
- \(y=2x+1\) について、xの変域 が 5<x≦7 のときの yの変域 を求めよ。
- \(y=5x+3\) について、xの変域 が -1≦x<4 のときの yの変域 を求めよ。
- \(y=-3x+2\) について、xの変域 が 2<x≦5 のときの yの変域 を求めよ。
- \(y=-2x-5\) について、xの変域 が -5≦x<-2 のときの yの変域 を求めよ。
- \(y=8x+3\) について、xの変域 が 1<x のときの yの変域 を求めよ。
- \(y=8x+3\) について、xの変域 が x<1 のときの yの変域 を求めよ。
- \(y=-2x+4\) について、xの変域 が 3<x のときの yの変域 を求めよ。
- \(y=-2x+4\) について、xの変域 が x<-2 のときの yの変域 を求めよ。
解説〈前編〉
簡易的なグラフを使っていますので、位置関係だけを参考にしてください。
グラフの傾きや切片の位置などは正確な比率で表記していません。
\(y=2x+1\) について、xの変域 が 5≦x≦7 のときの yの変域 を求めよ。
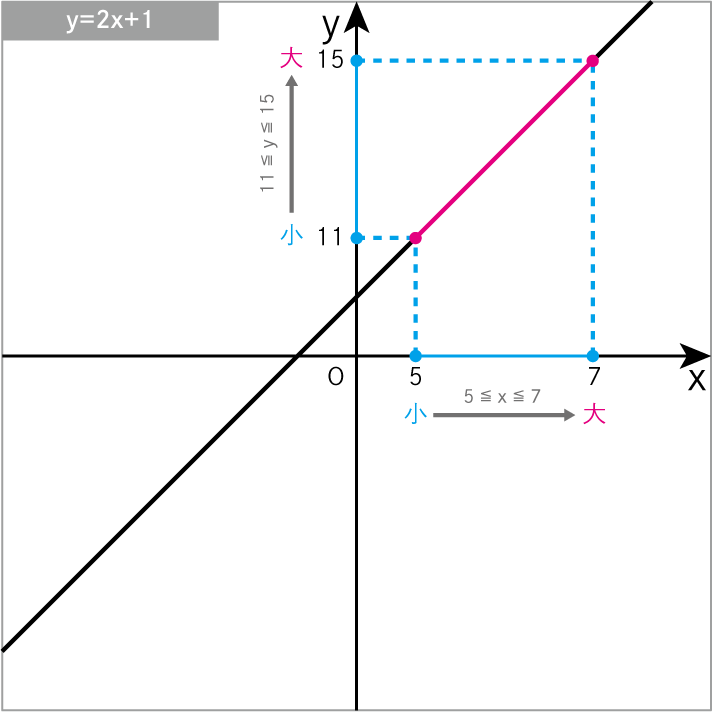
\(y=2x+1\)に\(x=5\)を代入
\(y=2 \times 5 +1 \\
y=10+1\\
y=11\)
\(y=2x+1\)に\(x=7\)を代入
\(y=2 \times 7 +1 \\
y=14+1\\
y=15\)
\(11≦y≦15\)
\(y=5x+3\) について、xの変域 が -1≦x≦4 のときの yの変域 を求めよ。
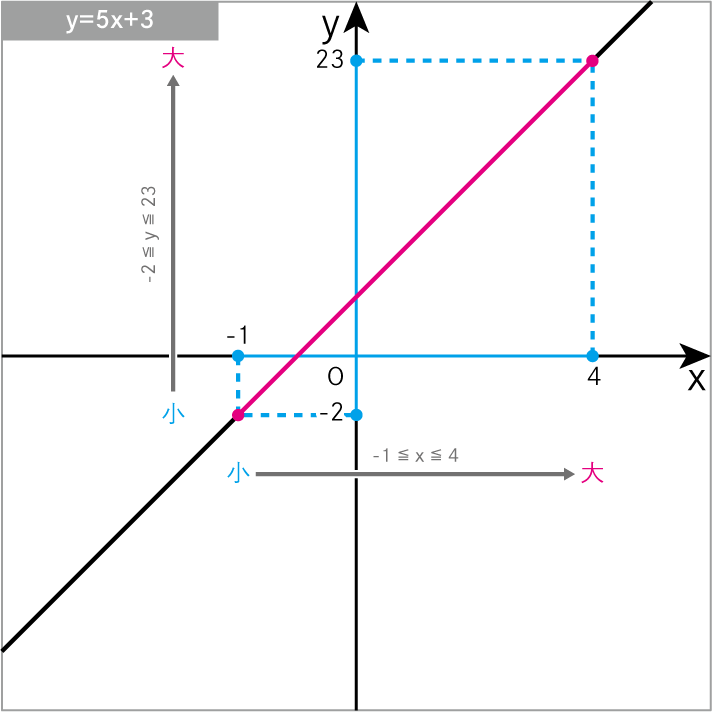
\(y=5x+3\)に\(x=-1\)を代入
\(y=5 \times (-1) +3 \\
y=-5+3\\
y=-2\)
\(y=5x+3\)に\(x=4\)を代入
\(y= \times 4 +3 \\
y=20+3\\
y=23\)
\(-2≦y≦23\)
\(y=-3x+2\) について、xの変域 が 2≦x≦5 のときの yの変域 を求めよ。
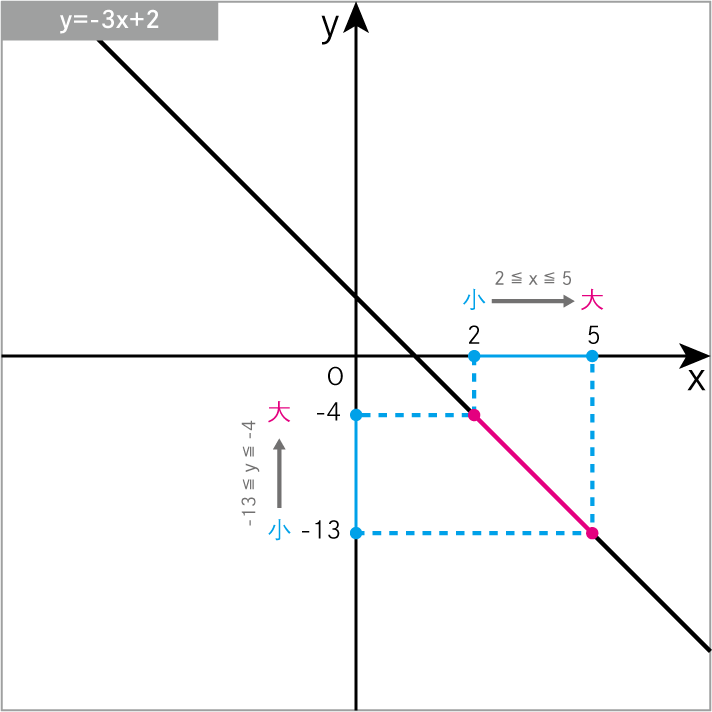
\(y=-3x+2\)に\(x=2\)を代入
\(y=-3 \times 2 +2 \\
y=-6+2\\
y=-4\)
\(y=-3x+2\)に\(x=5\)を代入
\(y=-3 \times 5 +2 \\
y=-15+2\\
y=-13\)
\(-13≦y≦-4\)
\(y=-2x-5\) について、xの変域 が -5≦x≦-2 のときの yの変域 を求めよ。
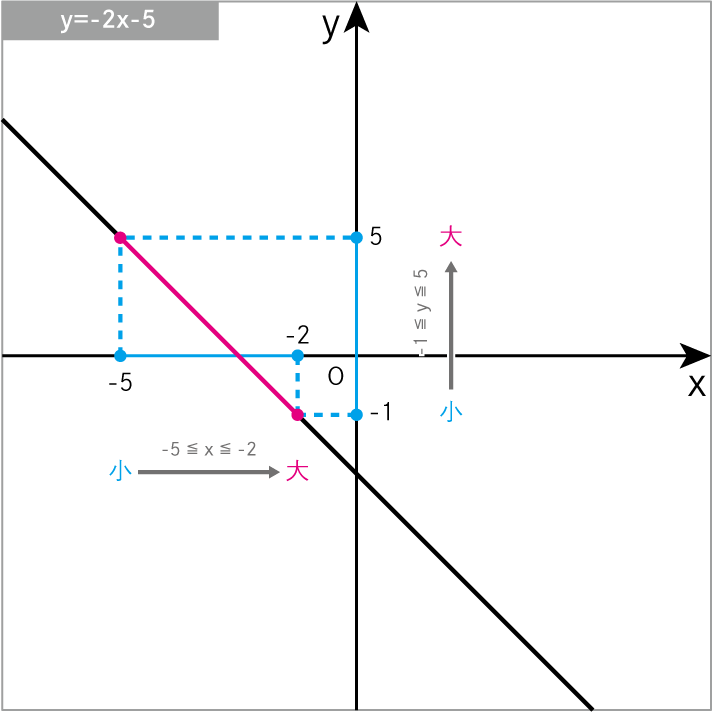
\(y=-2x-5\)に\(x=-5\)を代入
\(y=-2 \times (-5) -5 \\
y=10-5\\
y=5\)
\(y=-2x-5\)に\(x=-2\)を代入
\(y=-2 \times (-2) -5 \\
y=4-5\\
y=-1\)
\(-1≦y≦5\)
\(y=8x+3\) について、xの変域 が 1≦x のときの yの変域 を求めよ。
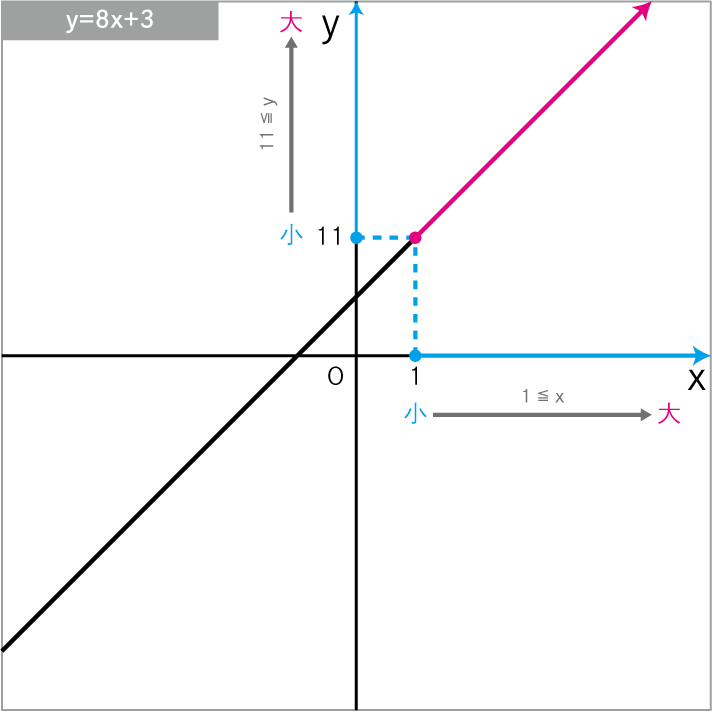
\(y=8x+3\)に\(x=1\)を代入
\(y=8 \times 1 +3 \\
y=8+3\\
y=11\)
\(11≦y\)
\(y=8x+3\) について、xの変域 が x≦1 のときの yの変域 を求めよ。
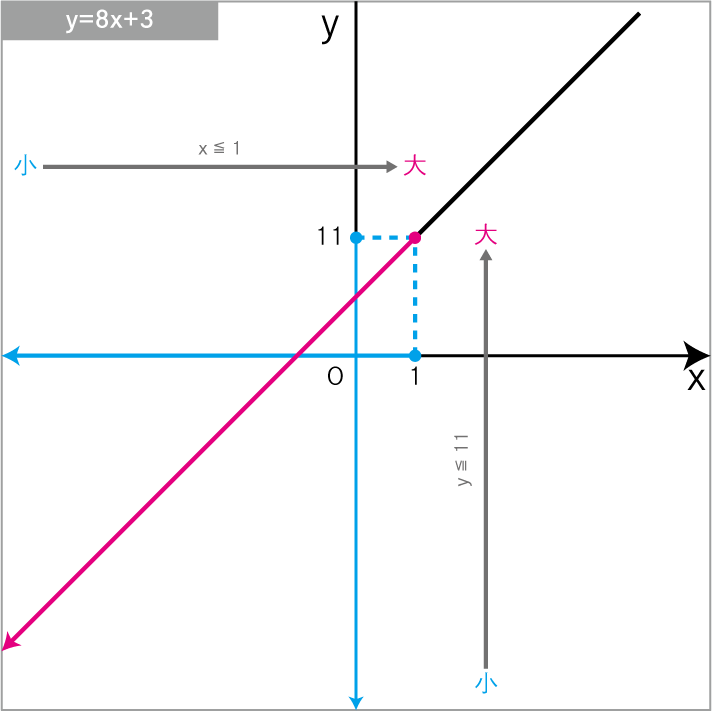
\(y=8x+3\)に\(x=1\)を代入
\(y=8 \times 1 +3 \\
y=8+3\\
y=11\)
\(y≦11\)
\(y=-2x+4\) について、xの変域 が 3≦x のときの yの変域 を求めよ。
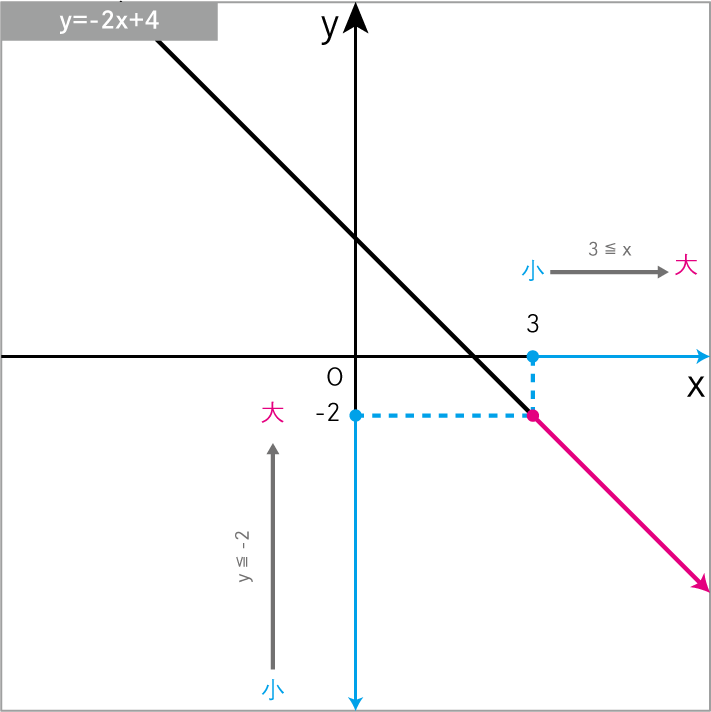
\(y=-2x+4\)に\(x=3\)を代入
\(y=-2 \times 3 +4 \\
y=-6+4\\
y=-2\)
\(y≦-2\)
\(y=-2x+4\) について、xの変域 が x≦-2 のときの yの変域 を求めよ。
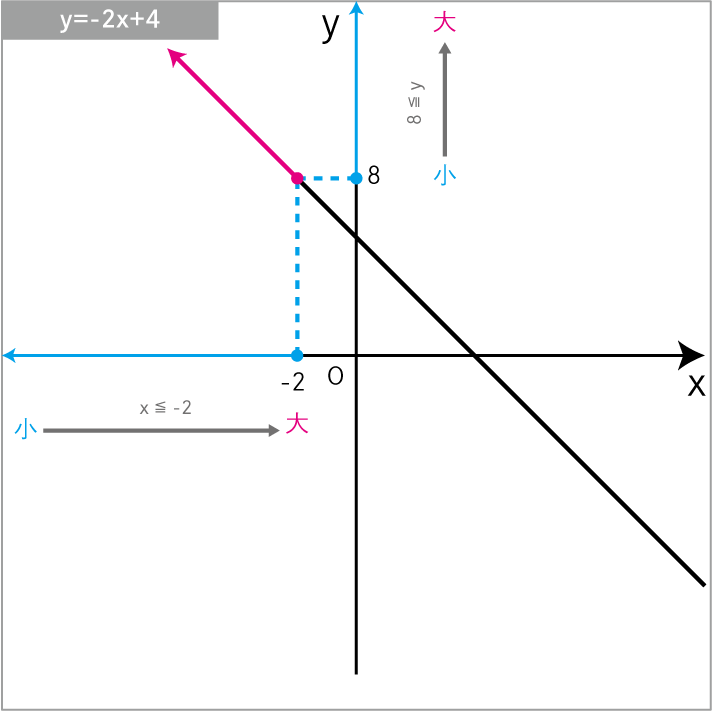
\(y=-2x+4\)に\(x=-2\)を代入
\(y=-2 \times (-2) +4 \\
y=4+4\\
y=8\)
\(8≦y\)
解説〈後編〉
\(y=2x+1\) について、xの変域 が 5<x≦7 のときの yの変域 を求めよ。
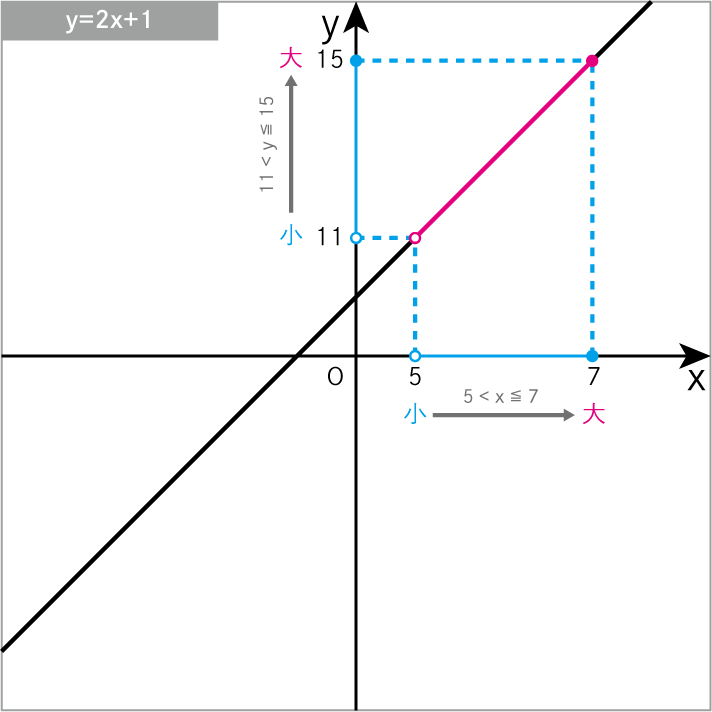
\(y=2x+1\)に\(x=5\)を代入
\(y=2 \times 5 +1 \\
y=10+1\\
y=11\)
\(y=2x+1\)に\(x=7\)を代入
\(y=2 \times 7 +1 \\
y=14+1\\
y=15\)
\(11<y≦15\)
\(y=5x+3\) について、xの変域 が -1≦x<4 のときの yの変域 を求めよ。
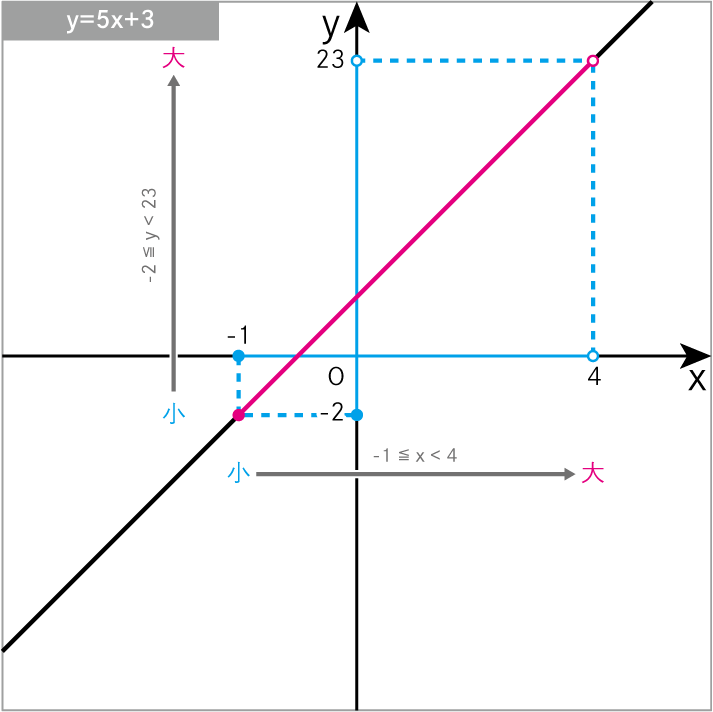
\(y=5x+3\)に\(x=-1\)を代入
\(y=5 \times (-1) +3 \\
y=-5+3\\
y=-2\)
\(y=5x+3\)に\(x=4\)を代入
\(y= \times 4 +3 \\
y=20+3\\
y=23\)
\(-2<y≦23\)
\(y=-3x+2\) について、xの変域 が 2<x≦5 のときの yの変域 を求めよ。
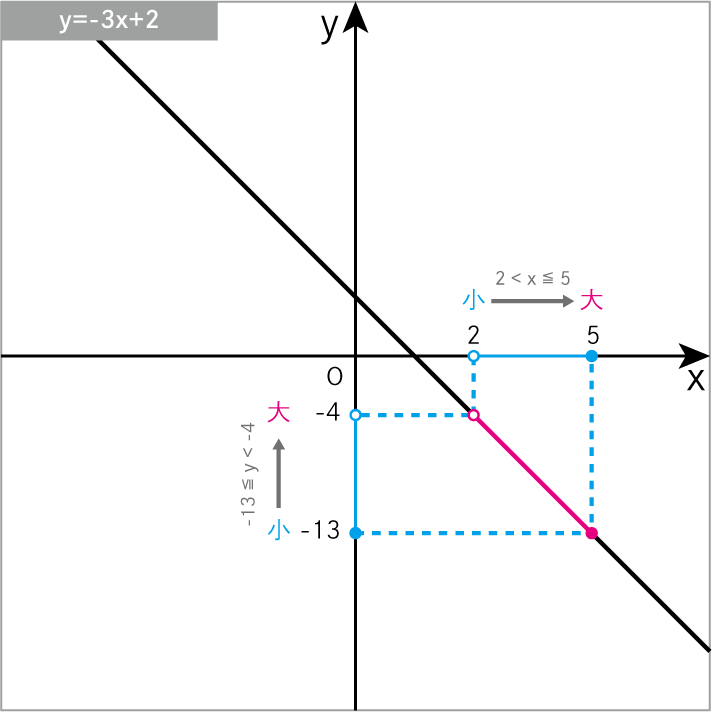
\(y=-3x+2\)に\(x=2\)を代入
\(y=-3 \times 2 +2 \\
y=-6+2\\
y=-4\)
\(y=-3x+2\)に\(x=5\)を代入
\(y=-3 \times 5 +2 \\
y=-15+2\\
y=-13\)
\(-13≦y<-4\)
\(y=-2x-5\) について、xの変域 が -5≦x<-2 のときの yの変域 を求めよ。
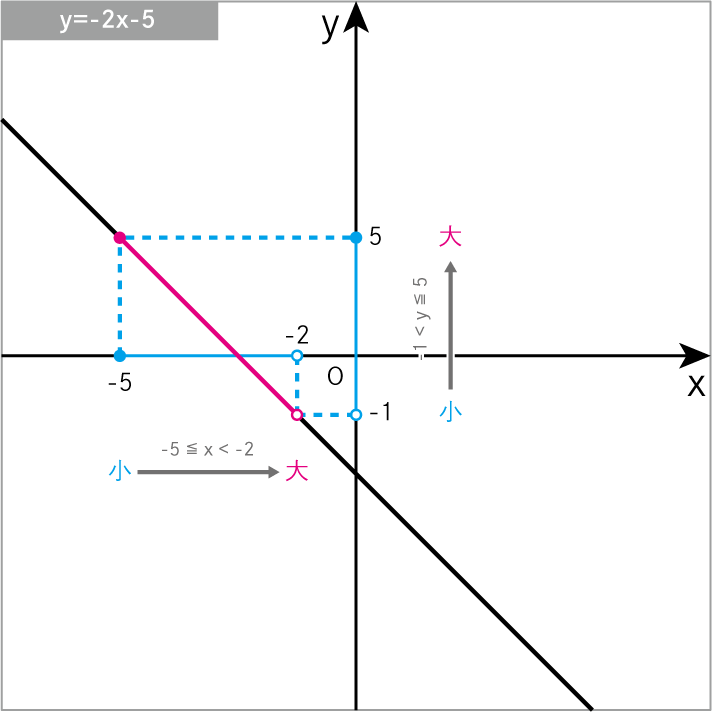
\(y=-2x-5\)に\(x=-5\)を代入
\(y=-2 \times (-5) -5 \\
y=10-5\\
y=5\)
\(y=-2x-5\)に\(x=-2\)を代入
\(y=-2 \times (-2) -5 \\
y=4-5\\
y=-1\)
\(-1<y≦5\)
\(y=8x+3\) について、xの変域 が 1<x のときの yの変域 を求めよ。
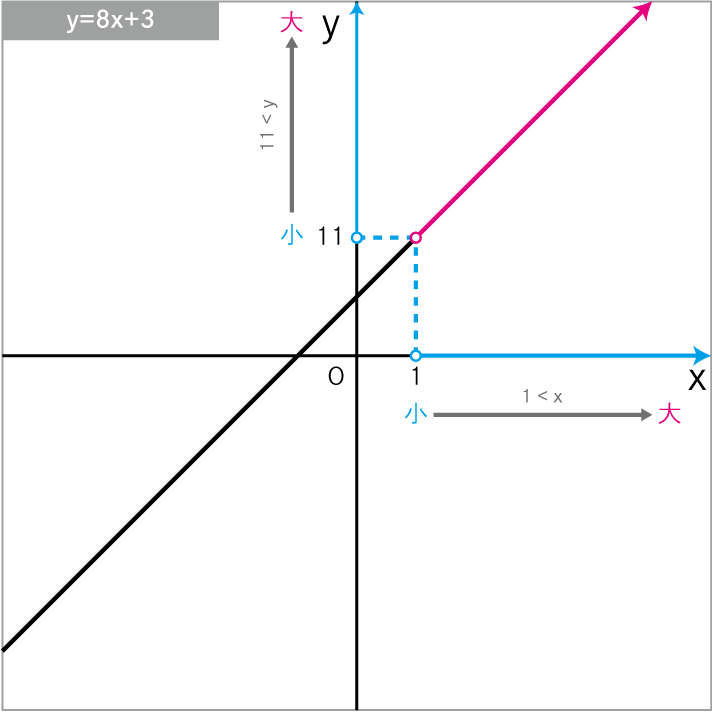
\(y=8x+3\)に\(x=1\)を代入
\(y=8 \times 1 +3 \\
y=8+3\\
y=11\)
\(11<y\)
\(y=8x+3\) について、xの変域 が x<1 のときの yの変域 を求めよ。
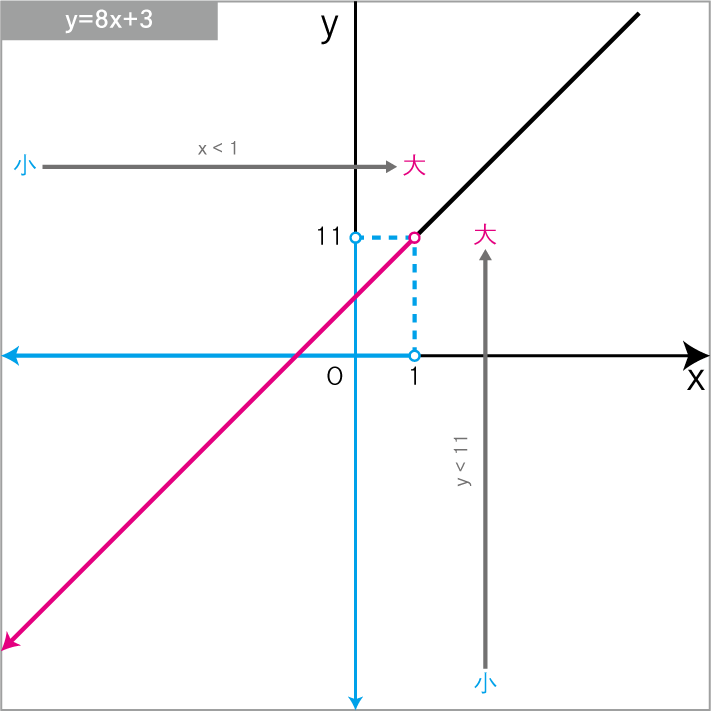
\(y=8x+3\)に\(x=1\)を代入
\(y=8 \times 1 +3 \\
y=8+3\\
y=11\)
\(y<11\)
\(y=-2x+4\) について、xの変域 が 3<x のときの yの変域 を求めよ。
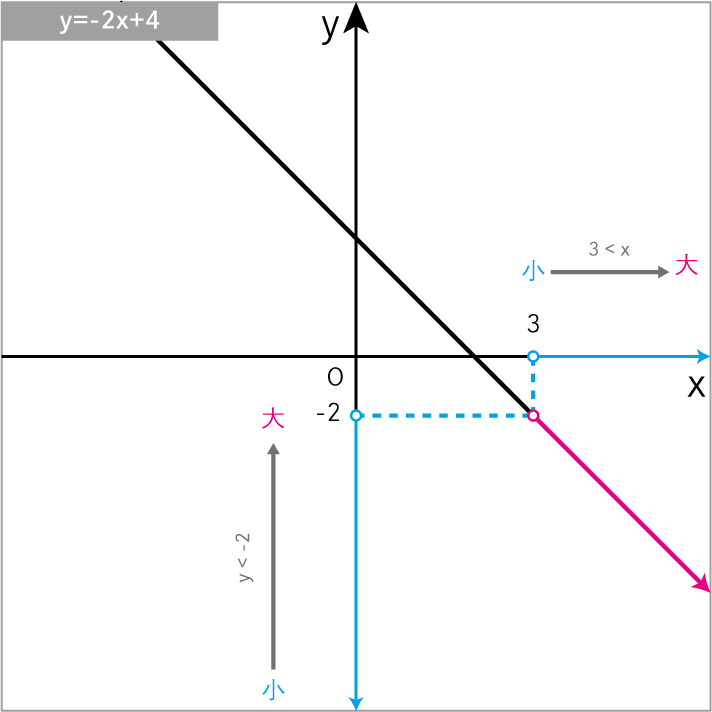
\(y=-2x+4\)に\(x=3\)を代入
\(y=-2 \times 3 +4 \\
y=-6+4\\
y=-2\)
\(y<-2\)
\(y=-2x+4\) について、xの変域 が x<-2 のときの yの変域 を求めよ。
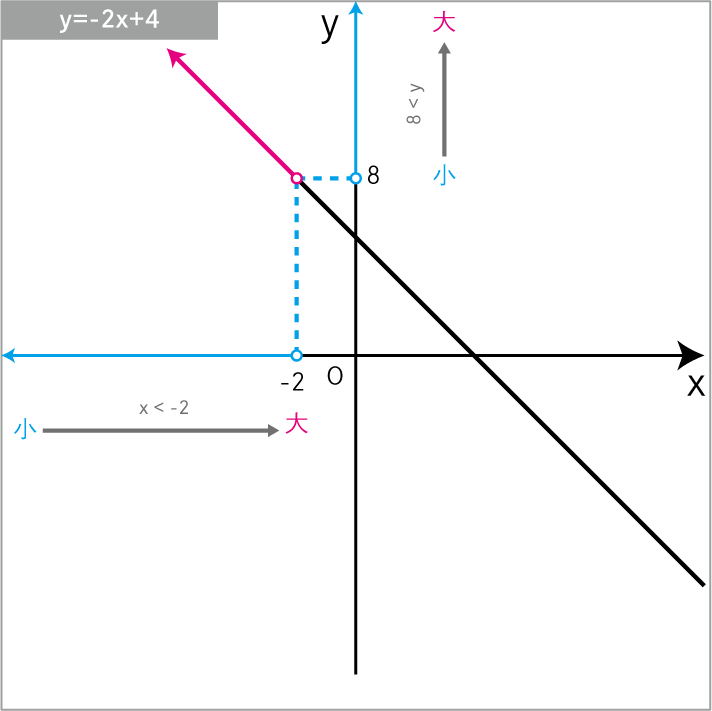
\(y=-2x+4\)に\(x=-2\)を代入
\(y=-2 \times (-2) +4 \\
y=4+4\\
y=8\)
\(8<y\)


コメント