後編の記事では、xとyの二つの変域を扱うことの解説をします。
変域や不等号について分からないことがあれば前編をみてください。
一次関数の変域を理解するために
一次関数の変域を理解するためのポイントは
- yの変域の理解
- <と≦の使い分け
- 変域の大小関係
この3つです。
ここが間違いやすいポイントでもあります。
解き方のコツは「グラフを描く」、これだけです。
グラフを書くだけで変域の問題はある程度解決するので、
面倒くさがらずにグラフを書きましょう。
yの変域の求め方
まずはyの変域のイメージを掴んでみましょう。
yの変域はグラフや表を使うと分かりやすいです。
以下の例題のyの変域について考えてみます。
y = 2x+1ついて xの変域 が 1≦x≦3 のときの yの変域 を求めよ
表を使って考える
y=2x+1を時給2円のアルバイトだと想定してみましょう。
労働時間(x)に対して2円(a)ずつ所持金(y)が増えていきます。
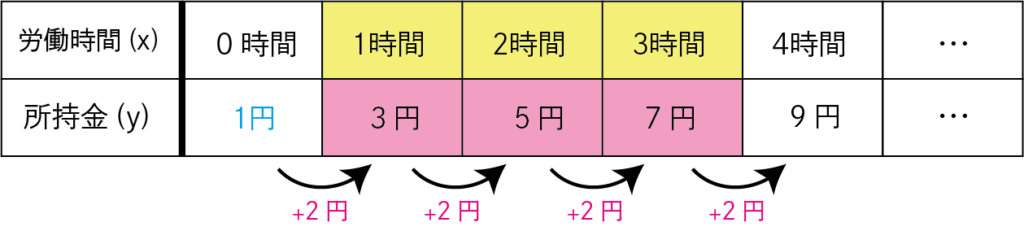
1≦x≦3の範囲を黄色で示しました。
それに対応する赤い範囲が yの変域 です。
「労働時間が1時間から3時間の間なら、所持金は3円から7円になる」
yの変域とはこんなイメージです。
これを変域として書くと、
1≦x≦3のとき、3≦y≦7 と書ける訳です。
グラフを使って考える
次にグラフでも見てみましょう。
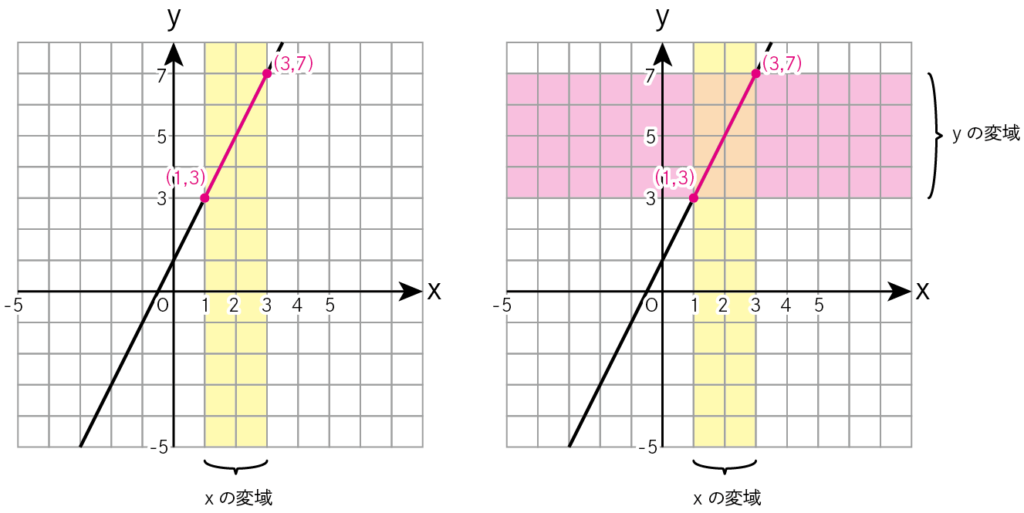
黄色い範囲がxの変域 1≦x≦3を表しています。
そうすると赤線部分がでてきました。
その赤線の縦の範囲がyの変域です。
右の図の赤い範囲が3から7なので、
こちらもyの変域を 3≦y≦7 と書けます。
「この赤線部分の先端はどこか」と探すのが、基本の考え方になります。
yの変域の求め方 A≦x≦B
グラフを描きながら、以下の例題を解いてみましょう。
y = 2x+1ついて xの変域 が 1≦x≦3 のときの yの変域 を求めよ
まずはx軸とy軸を描きましょう。
次に大体で良いのでy = 2x+1の直線を描き、
xの変域である1≦x≦3を書き込みましょう。
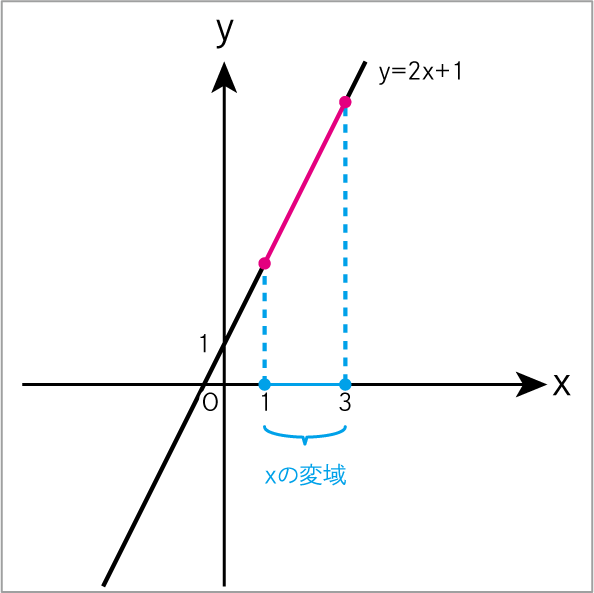
すると、xの変域によって赤線部分が出来ます。
その赤線の先端のy座標を求めましょう。
それらは代入で求めることができます。
y=2x+1にx=1を代入
\(y=2 \times 1+1\\
y=3\)
y=2x+1にx=3を代入
\(y=2 \times 3+1\\
y=7\)
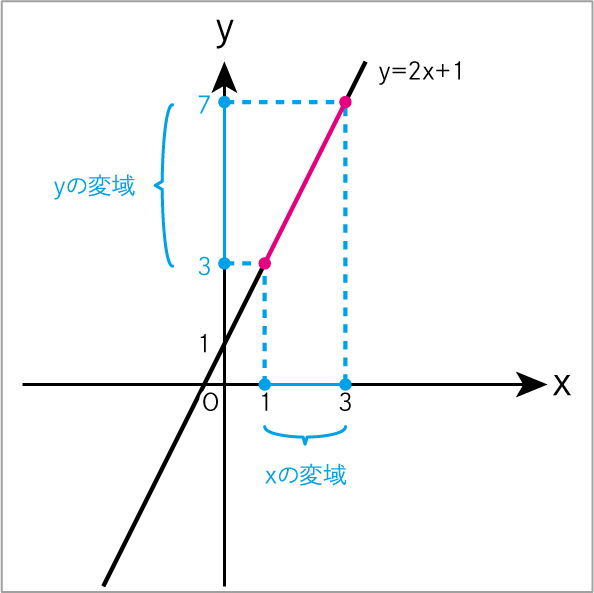
y=3、y=7となったので、
yの変域は 3≦y≦7 と分かりました。
yの変域の求め方 A≦x
以下の問題を考えてみましょう。
- y = 2x+1ついて xの変域 が 1≦x のときの yの変域 を求めよ
この場合も、
直線の式にxの値を代入することでyの変域を求めることができます。
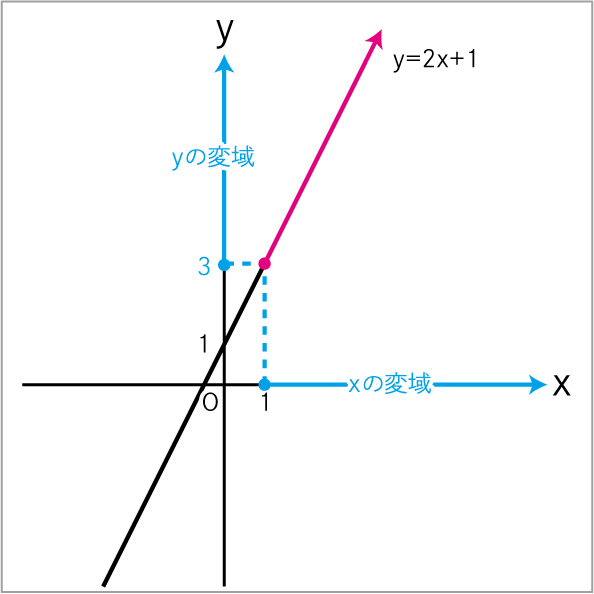
1≦x (xが1以上)なので、赤線はy=3が一番下です。
そこから上にずっと伸びていきます。
y=3から上全部がyの変域となります。
よって、yの変域は3≦y (yは3以上) です。
yの変域の求め方 x≦B
y = 2x+1ついて xの変域 が x≦3 のときの yの変域 を求めよ
x≦1 のときの yの変域
x≦1 (xが1以下)なので、赤線はy=3が一番上です。
そこから下にずっと伸びていきます。
y=3から下全部がyの変域となります。
よって、yの変域はy≦3 (yは3以下) です。
変域の大小関係
変域では、不等号の向きと数字の大小関係がとても大事です。
グラフと大小関係 A≦x≦B
xの値は右に行くほど大きくなり、左に行くほど小さくなります。
yの値は上に行くほど大きくなり、下に行くほど小さくなります。
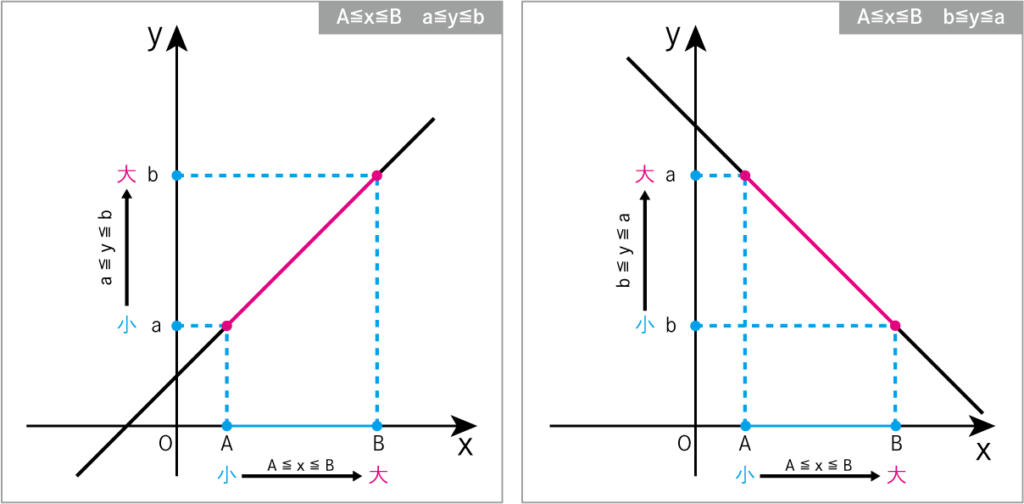
小→大の順で書くので、
xの変域はA≦x≦Bと書けます。
また、yの範囲では小さい値がa、大きい値がb。
a≦y≦bとなります。
グラフと大小関係 A≦x x≦B
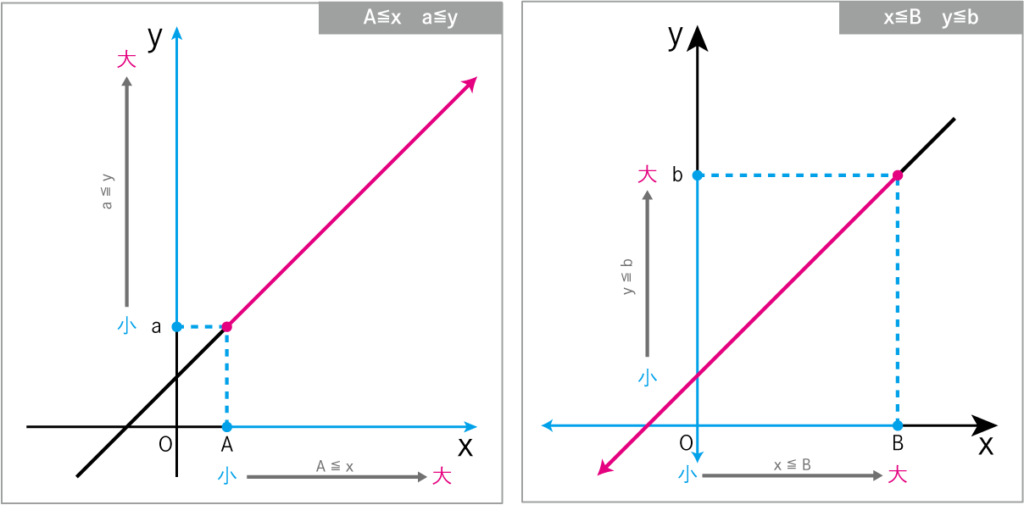
A≦xのとき、aがyの範囲内の最小になるので、
a≦yとなります。
x≦Bのとき、bがyの範囲内の最大になるので、
y≦bとなります。
適切な向きの不等号を書けるようにしましょう。
注意すること
数字の大小と不等号の向きを合わせる
3≦x≦1と書いてはいけません。
xは3以上、1以下という意味になり、矛盾が生じてしまいます。
不等号の向きと数字の大小関係を合わせましょう。3≦x≦1 → 1≦x≦3
余計な情報を書かない
1≦x≧3も書いてはいけません。
xは1以上、かつ3以上という意味になります。
3以上は1以上に含まれるので、書く必要がありません。
余計な情報は書かないようにしましょう
1≦x≧3 → 1≦x , 3≦x → 1≦x
<の≦の使い分け
グラフでは
○で表される点は、その値を含まない(超過、未満)
●で表される点は、その値を含む(以下、以上)
という意味で使われます。
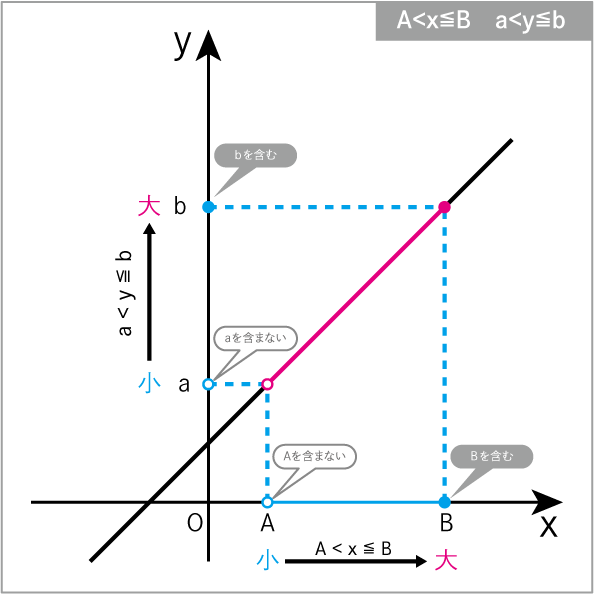
このグラフの場合、xの変域はA<x≦Bなので
A<x(Aを含まない)は○、
x≦B(Bを含む)は●となっています。
x=Aは○なので対応するy=aも○、
x=Bは●なので対応するy=bも●となり、
yの変域はa<y≦bと書くことができます。
Aを「含まない」なら、それに対応するaも「含まない」、
Bを「含む」なら、それに対応するbも「含む」ということです。
対応するxとyの値と、「含む」「含まない」の関係が一致することに注意。
不等号の使い分け A<x≦B
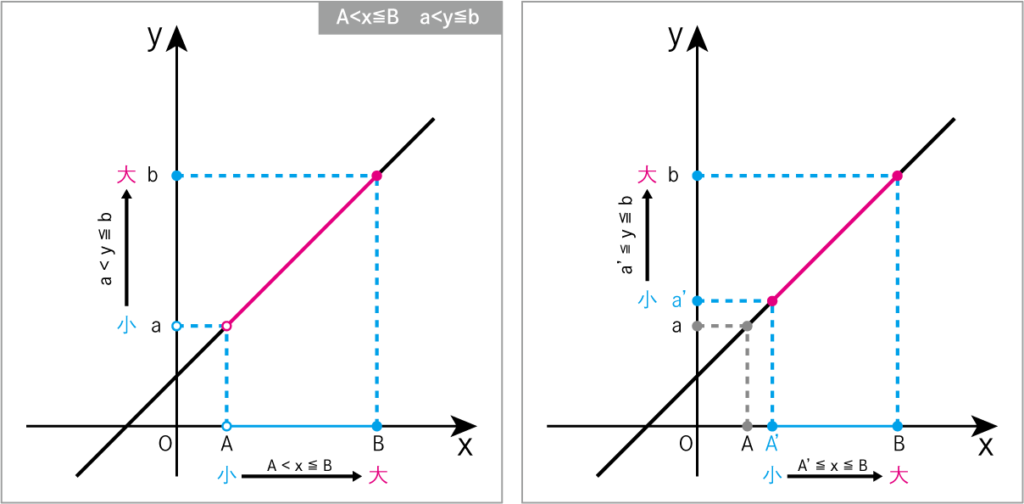
Aを含まないとは、
Aが仮に1とした時、A’は1.00…001のような、
限りなく1に近い値というイメージです。
1.00…001のような無限に続く数字を、
1という数字を借りて、1<xのように表現しています。
また、x=A’に対応するyの値はaにならないので、
yの変域でもaを含みません。
不等号の使い分け A≦x<B
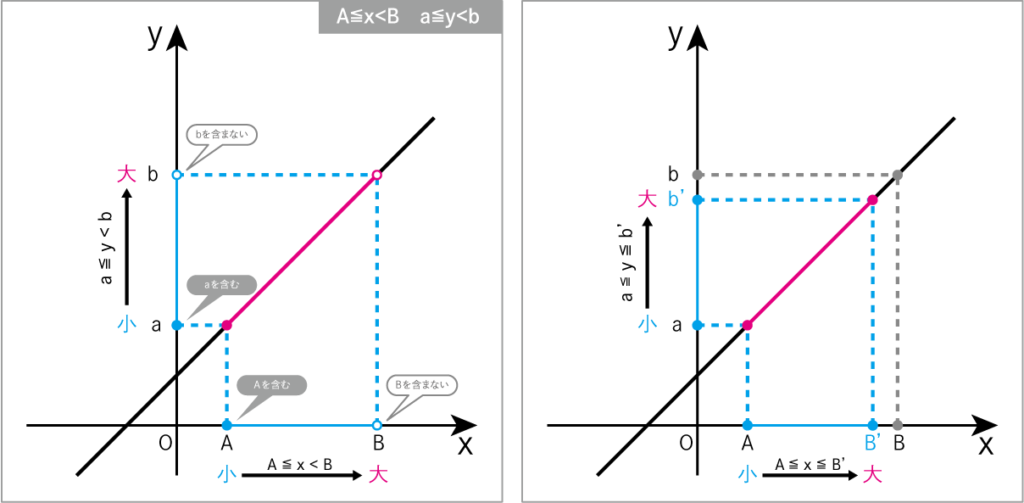
Bを含まないとは、
Bが仮に2とした時、B’は1.99…999のような、
限りなく2に近い値というイメージです。
1.99…999のような無限に続く数字を、
2という数字を借りて、2<xのように表現しています。
また、x=B’に対応するyの値はbにならないので、
yの変域でもbを含みません。
「変化の割合」がマイナスの時は注意
「変化の割合」がマイナスの時は注意がすこし必要です。
大小関係
以下の例題について考えてみましょう。
- y = -2x+1ついて xの変域 が 1≦x≦3 のときの yの変域 を求めよ
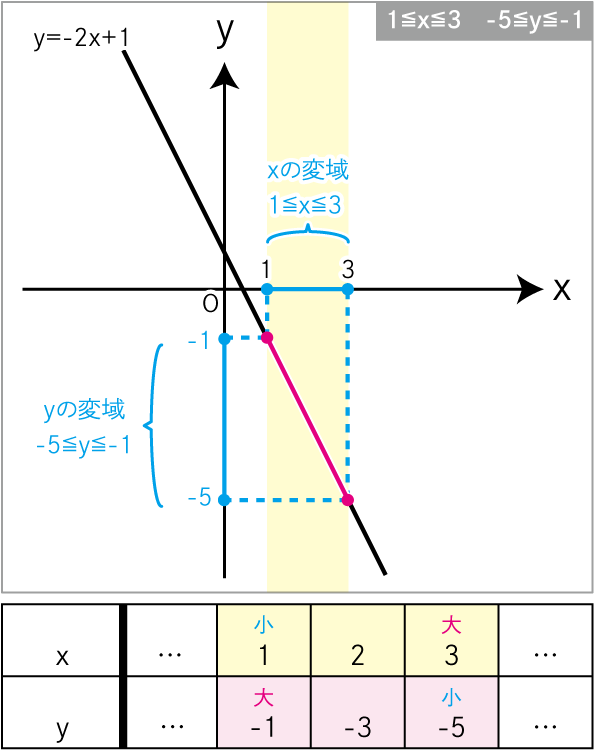
yは-1→-5と変化しています。
しかし、このyの変域を-1≦y≦-5と書くと間違いです。
-5≦y≦-1
と書かなければなりません。
なぜならば、変域は大小関係で表す範囲だからです。
表やグラフの向きとは関係ありません。
数字の大小関係と不等号の向きを合わせましょう。
間違いやすい理由
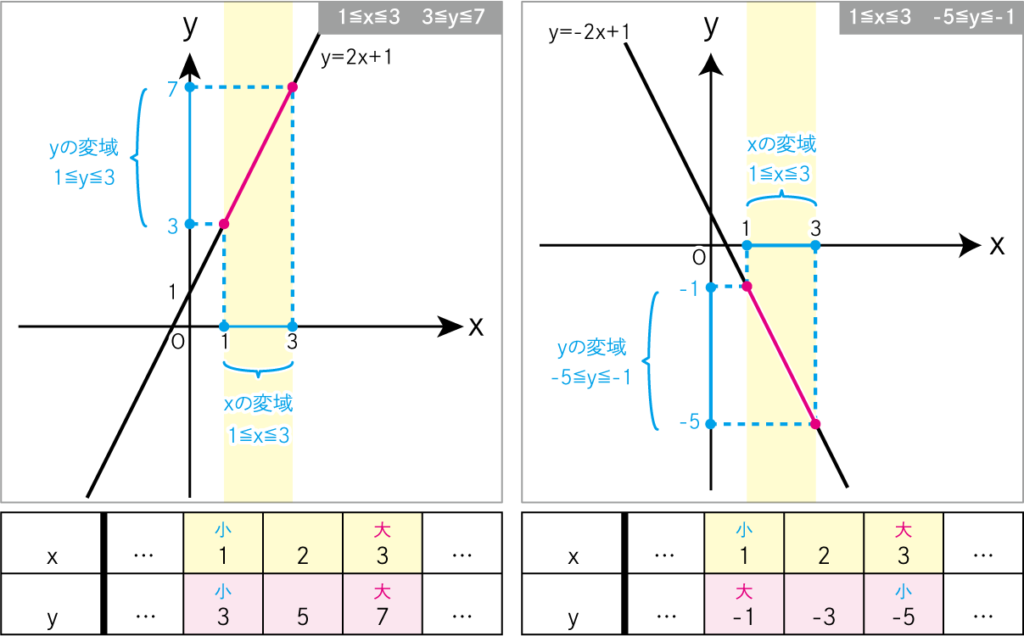
「変化の割合」がプラスの時、xとyはそれぞれ小→大と変化していますが、
「変化の割合」がマイナスの時、xが小→大に対して、yが大→小です。
「変化の割合」によって、yの値の大小関係が変わるということです。
間違いやすいところですので、気をつけましょう。
不等号の使い分け
「変化の割合」がマイナスになると、不等号の位置も変わります。
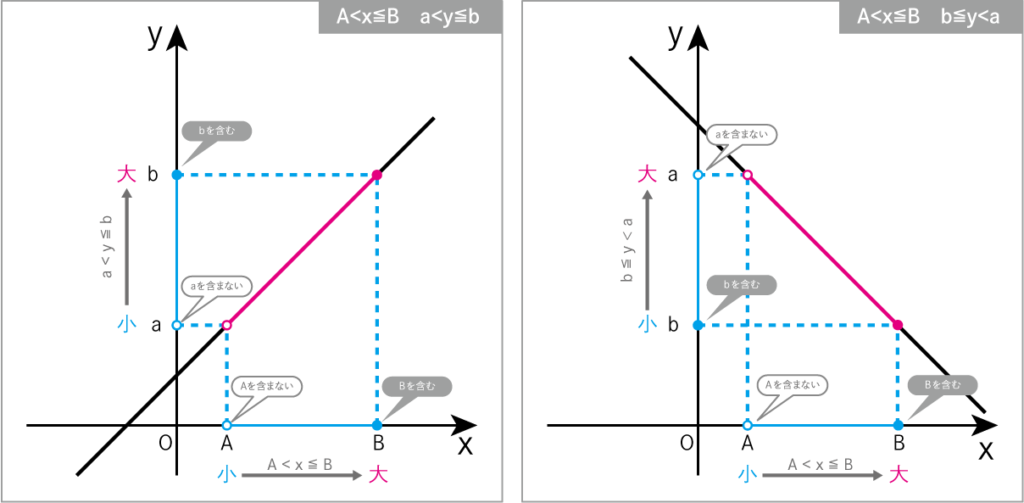
「変化の割合」がプラスの時、
A<x≦Bのyの変域はa<x≦bであるのにたいして、
「変化の割合」がマイナスの時、
A<x≦Bのyの変域はb≦y<aとなります。
対応するxとyの値は「含む」「含まない」の関係が一致します。
それは「変化の割合」がマイナスになっても変わりません。
まとめ
xとyの二つの変域においても、注意するポイントは
大小関係と不等号の向きを合わせることと、
不等号の種類を一致させることです。
今回は解説に加えませんでしたが、
逆にyの変域からxの変域を求めることも可能です。
別の機会に解説したいと思います。
xの変域からyの変域を計算する例題集をつくったのでやってみてください!


コメント