前編では計算をあまり使わずに解説してきました。
後編では、実際にどのような計算をするのかを解説していきます。
直線の式の計算ステップ
直線の式を求め方は3つあり、
それぞれで計算のステップが違うことに注目してください。
- 「2点の座標」で求める → ①「変化の割合」を求める ②\(y=ax+b\)に代入する
- 「変化の割合」と「1点の座標」で求める → \(y=ax+b\)に代入する
- 「切片」と「1点の座標」で求める → \(y=ax+b\)に代入する
違いがあるのは「2点の座標」で求めるときの〈①「変化の割合」を求める〉だけです。
〈①「変化の割合」を求める〉方法さえ分かれば、直線の式はなんとかなります。
「変化の割合」の計算も、代入する計算も難しくないのでついてきてください。
「変化の割合」を求める方法は2つ
- a.〈xとyの増加量〉で「変化の割合」を求める
- b.〈連立方程式〉で「変化の割合」を求める
この2つの方法のうち、どちらかはしっかりと覚えましょう。
xとyの増加量
「変化の割合」を求めるには増加量という考え方が必要になります。
増加量とは、「どれだけ変化したか」です。
増加と書いていますが、〈プラス〉だけではなく、〈マイナス〉の時もあります。
(1,3)、(3,7)を通る直線の式を求めよ。
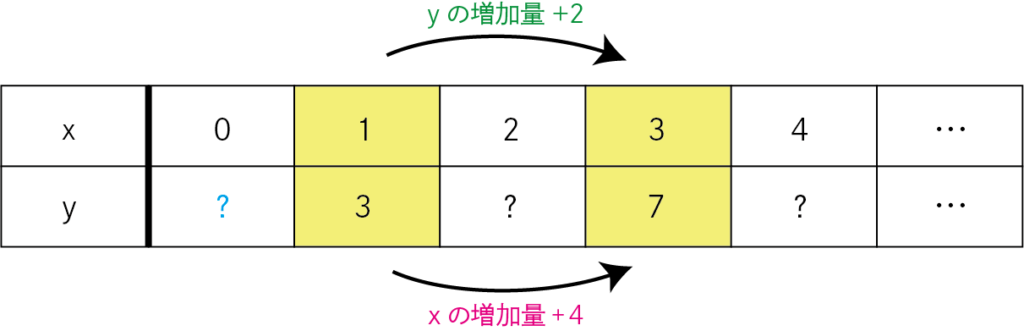
例えばこの(1,3)と(3,7)の座標の間で、
xは+2増加し、yは+4増加しています。
この変化の差が増加量と呼ばれるものです。
「変化の割合」はこのxとyの増加量を使って求めます。
「2点の座標」から「変化の割合」を求める
さて、ここからが本題です。
「変化の割合」の求め方を以下の例題を使って解説します。
(1,3)、(3,7)を通る直線の式を求めよ。
a.〈xとy増加量〉で「変化の割合」を求める
「2点の座標」から「変化の割合」を求める式

〈yの増加量〉を〈xの増加量〉で割ると「変化の割合」になります。
上の式に、(1,3)、(3,7)を代入します。
青い四角の中に、それぞれの座標を入れましょう。

分母(下)がxの値、分子(上)がyの値です。
今回の場合、分母の2がxの増加量、分子の4がyの増加量です。
この計算を解くと、「変化の割合」が2であることが分かります。
【補足】
今回、(3,7)を式の左側に書きました。
xの値が大きい座標を左側に書くのが一般的です。
理由は分母にマイナスをつけずに計算できるからです。
左右が逆でも計算結果は同じなので
あまり気にしなくても大丈夫です。
ただし、xとyの上下の位置だけは必ず気をつけてください。
計算結果が変わってしまいます。
左右逆にした場合
\(a\)(変化の割合)
\(
\large{
=\frac{(3)-(7)}{(1)-(3)}\\
=\frac{-4}{-2}=2}
\)
計算イメージ
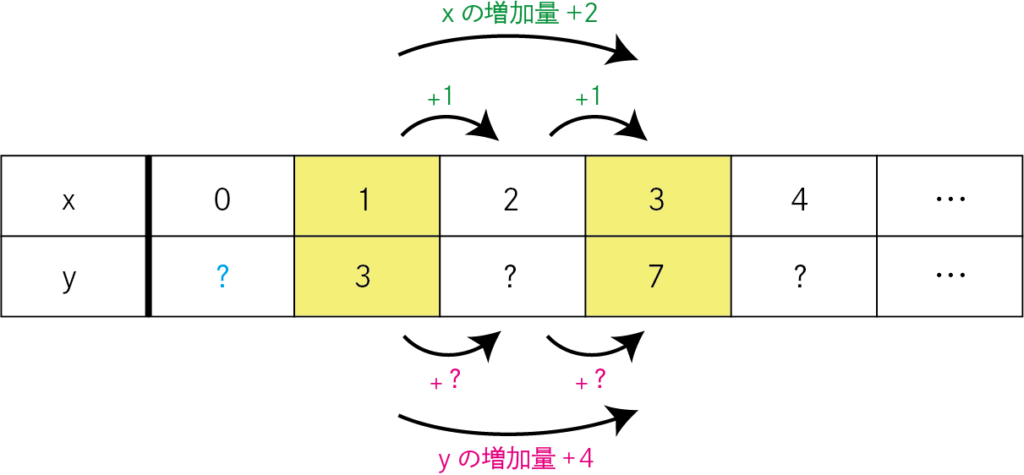

xが2回変化する中で、yが4変化しています。
そのときの+?の1回分の変化について考えます。
これは前半の記事で解説したものと同じ考え方です。
b.〈連立方程式〉で「変化の割合」を求める
次に連立方程式で計算する方法を紹介します。
まず\(y=ax+b\)に(1,3)、(3,7)をそれぞれ代入した式を用意します。
\(\cases{3=1a+b \cdots ①\\7=3a+b \cdots ②}\)
※分かりやすいように1を省略せずに書いています
この2つの式で連立方程式を解きます。
②-①より
\(
\begin{eqnarray}
7 &=& 3a+b\\
-)3 &=& 1a+b\\
\hline
4 &=& 2a\\
2 &=& a\\
\\
a &=& 2
\end{eqnarray}
\)
「変化の割合」は2となりました。
計算イメージ
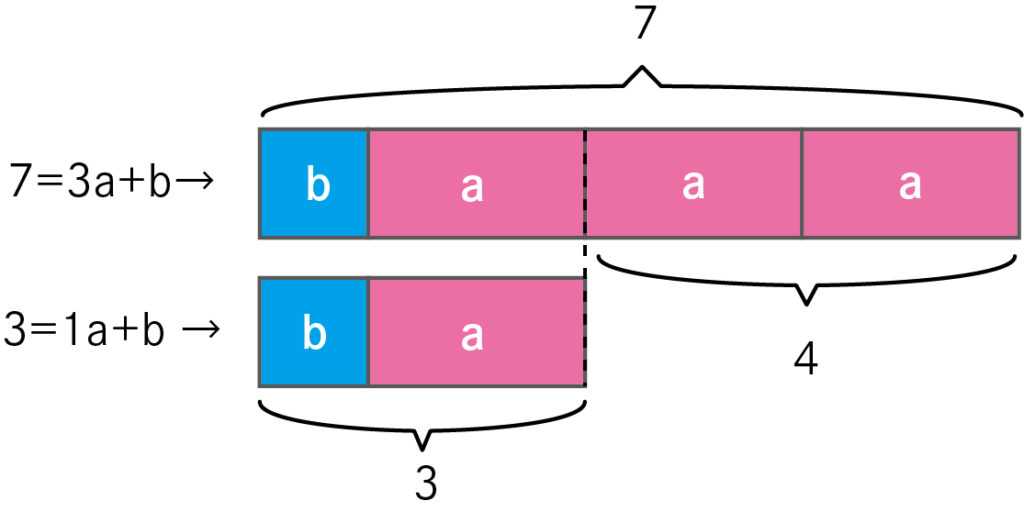
\(y=ax+b\)に(1,3)、(3,7)をそれぞれ代入した式で連立方程式を解くと、
a(変化の割合)の1つあたりの数値が逆算できます。
\(y=ax+b\)に代入する
「変化の割合」か「切片」が分かり、さらに座標が1点以上分かっている時、
\(y=ax+b\)にそれぞれ代入して計算すると直線の式を求めることができます。
「2点の座標」で直線の式を求める
(1,3)、(3,7)を通る直線の式を求めよ。
上記の問題は、「変化の割合」が2であることが先ほどの計算によってわかりました。
この場合は、\(y=ax+b\)に「変化の割合」とどちらか1点の座標を代入します。
\(y=ax+b\)に
a(変化の割合)=2、(1,3)を代入
\(3=2\times1+b
\\3=2+b
\\3-2=b
\\1=b
\\b=1
\)
\(y=ax+b\)に
a(変化の割合)=2、(3,7)を代入
\(7=2\times3+b
\\7=6+b
\\7-6=b
\\1=b
\\b=1
\)
どちらの座標を代入しても、計算結果は同じになります。
計算が簡単な方を代入しましょう。
「変化の割合」が2、「切片」が1なので、
\(y=2x+1\)となります。
代入の計算イメージ
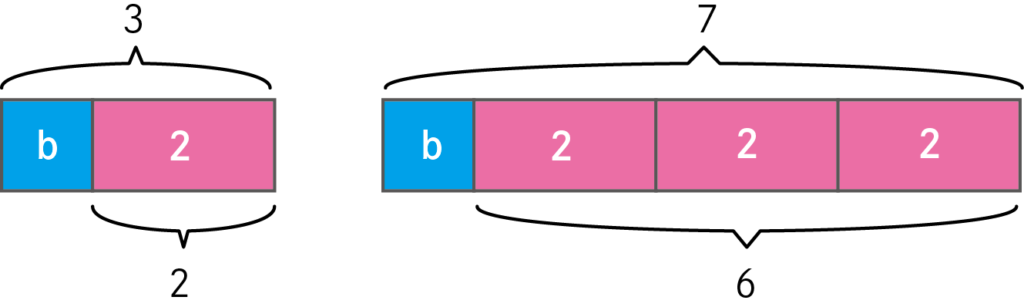
〈\(3=2\times1+b\)〉と〈\(7=2\times3+b\)〉を図にするとこのようになる。
逆算してb(切片)を求めます。
「変化の割合」と「1点の座標」で求める
変化の割合が2で、(4,9)を通る直線の式を求めよ。
\(y=ax+b\)に「変化の割合」と1点の座標を代入しましょう。
\(y=ax+b\)に
a(変化の割合)=2、(4,9)を代入
\(9=2\times4+b
\\9=8+b
\\9-8=b
\\1=b
\\b=1
\)
よって、
「変化の割合」が2、「切片」が1なので、
\(y=2x+1\)となります。
代入の計算イメージ
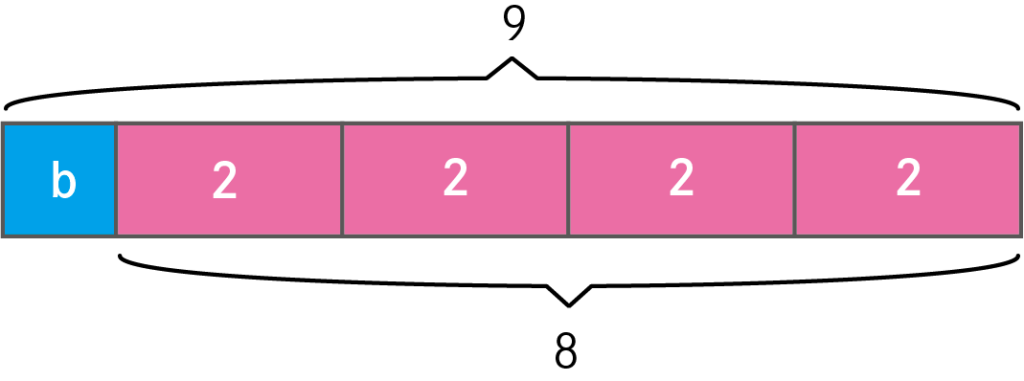
〈\(9=2\times4+b\)〉を図にするとこのようになります。
逆算してb(切片)を求めます。
「切片」と「1点の座標」で求める
切片が1で、(4,9)を通る直線の式を求めよ。
\(y=ax+b\)に「切片」と1点の座標を代入しましょう。
\(y=ax+b\)に
b(切片)=1、(4,9)を代入
\(9=a\times4+1
\\9=4a+1
\\9-1=4a
\\8=4a
\\4a=8
\\a=2
\)
よって、
「変化の割合」が2、「切片」が1なので、
\(y=2x+1\)となります。
代入の計算イメージ
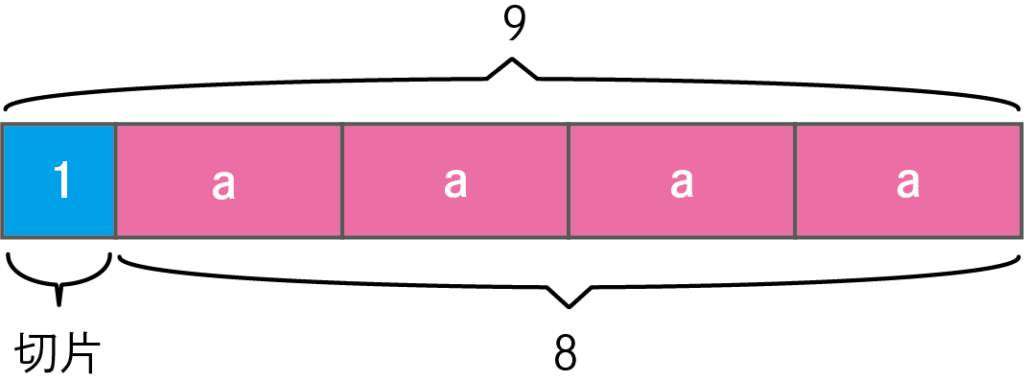
〈\(9=a\times4+1\)〉を図にするとこのようになります。
「変化の割合」1つ分の値を逆算します。
まとめ
まずは、変化の割合を求められるようになりましょう。
- a.〈xとyの増加量〉で「変化の割合」を求める
- b.〈連立方程式〉で「変化の割合」を求める
一次関数が苦手な人はひとまずこれに集中してみてください。
「変化の割合」が求められるようになれば、あとは代入して計算するだけです。


コメント