一次関数では〈直線の式 \(y=ax+b\)〉を求めることがとても多いです。
一次関数が苦手という人の多くはまずここにつまづいているのではないでしょうか。
この記事では小難しい計算を抜きにして、\(y=ax+b\)の求め方を解説します。
やっていることはとても簡単なのでついてきてください。
「直線の式を求める」ために
直線の式\(y=ax+b\)を求めるためのキーワードは以下の3つ。
「変化の割合」と「切片」と「点の座標」です。
一次関数が苦手な人は、まずはこのキーワードに注目してみましょう。
「変化の割合」と「切片」が分かればいい
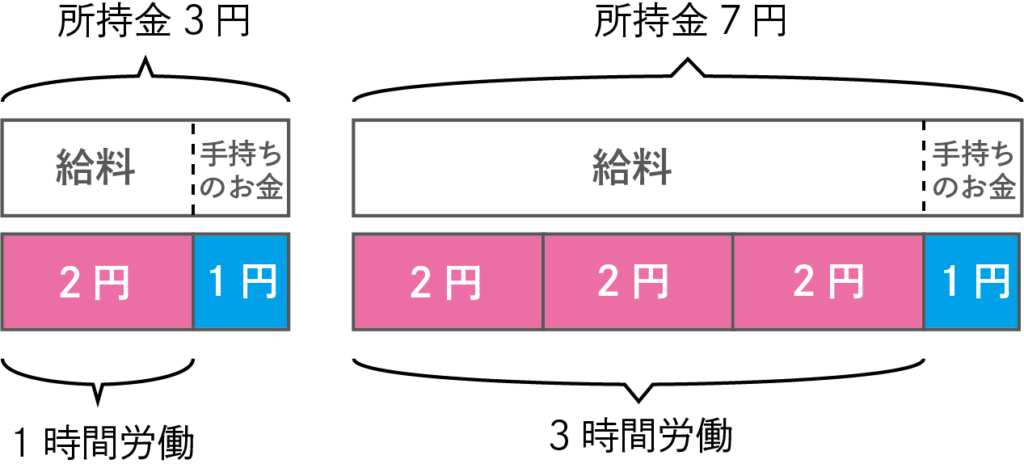
次の表を見てください。想像しやすいように表には単位(時間と円)をつけました。
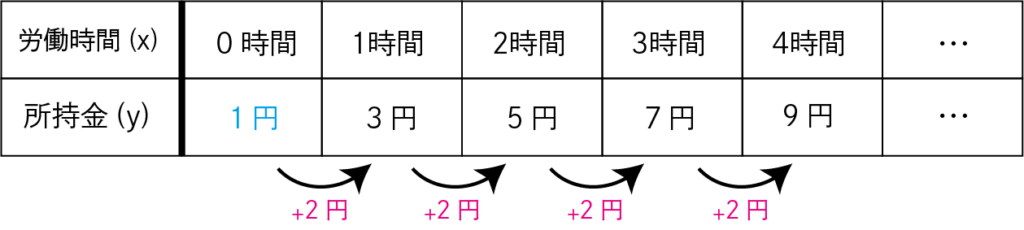
例えば、時給が2円のアルバイトがあったとして、働く前に1円所持していたとしましょう。
このときの「変化の割合」は2で、「切片」は1となり、\(y=2x+1\)と書けます。
「直線の式\(y=ax+b\)を求める」とは、「変化の割合」と「切片」を答えることです。
このように、直線の式でやることはとてもシンプルなのです。
「点の座標」を理解しよう

\(y=2x+1\)の表をグラフにすると上のような直線になります。
直線上に点がいくつかありますよね。
点の位置を表現したものが「座標」です。
この「点の座標」は表の上下の数字の組み合わせです。
例えばこの表で言うと、
〈1時間と3円〉は\(x=1\),\(y=3\)であり、(1,3)の点を表したものです。
この「点の座標」を使うことで、「変化の割合」や「切片」を求められるようになります。
直線の式を求める考え方
直線の式の求め方は大きく分けて3つあります。
- 「2点の座標」で求める
- 「変化の割合」と「1点の座標」で求める
- 「切片」と「1点の座標」で求める
この3つの方法が分かれば、直線の式が求めます。
1番目のやり方が分かるとどれも解けるようになります。
なぜかというと、
2番目と3番目の方法は、1番目の計算過程とほぼ同じだからです。
1.「2点の座標」から直線の式を求める《重要》
「2点の座標」から直線の式を求める、以下のような例題を考えてみます。
(両方とも同じ直線の式についての問題です。)
- 2点 (1,3)、(3,7)を通る直線の式を求めよ。
- \(x=1\)のとき\(y=3\)、\(x=3\)のとき\(y=7\)である直線の式を求めよ。
抽象的で分かりづらいので表にしてみましょう。
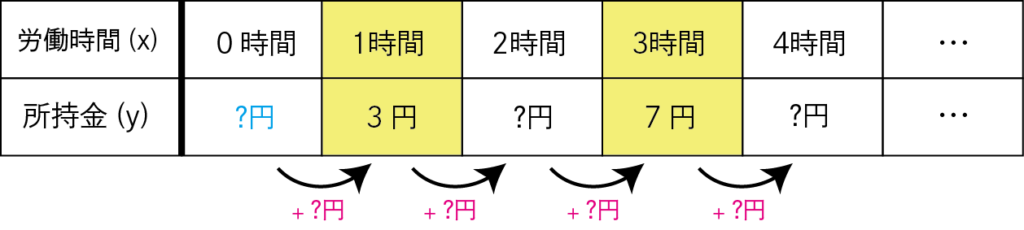
2点 (1,3)、(3,7)とは、
この表で言うところの〈1時間のとき3円〉と〈3時間のとき7円〉です。
「2点の座標」が分かっているとはこういう状況です。
この表の赤字部分の「変化の割合」と青字部分の「切片」が分かる、
それが直線の式を求めると言うことです。
「変化の割合」を求める
まずは変化の割合を求めてみましょう。
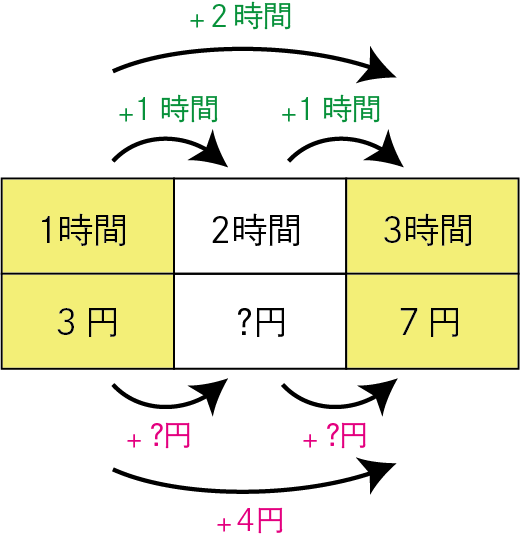
〈1時間〉から〈3時間〉の間に注目してください。
2時間で4円増加しているのが分かるでしょうか。
つまり1時間で2円増加しています。
よって「変化の割合」は2になります。
それぞれの差を求めて、割り算するだけ。
「2点の座標」が分かると「変化の割合」が簡単に分かってしまうのです。
「切片」を求める
次に切片を求めてみましょう。
先ほど「2点の座標」から「変化の割合」がわかりました。
「変化の割合」が分かると「切片」が逆算できます。
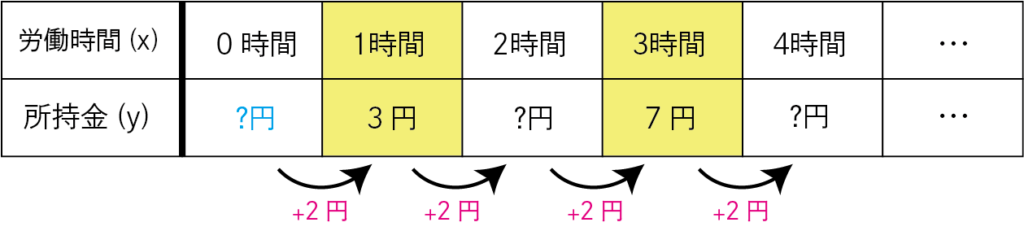
1時間労働のとき、?円+2円=3円になっています。
つまり、もとのお金(切片)は1円。
3時間労働のとき、?円+6円=7円になっています。
つまり、もとのお金(切片)は1円。
このように「切片」を逆算して考えることができます。
それぞれの値を代入する
「変化の割合」と「切片」がそれぞれ分かったので、あとは\(y=ax+b\)に代入しましょう!
「変化の割合」が2で、「切片」が1でしたので、\(y=2x+1\)と書けます。
2.「変化の割合」と「1点の座標」で求める
「変化の割合」と「1点の座標」から直線の式を求める、以下のような例題を考えてみます。
- 変化の割合が2でx=4のとき、y=9の直線の式を求めよ。
- 傾きが2で(4,9)を通る直線の式を求めよ。
この問題を表に直すと、
「変化の割合」と〈4時間のとき9円〉が分かっている状態です。
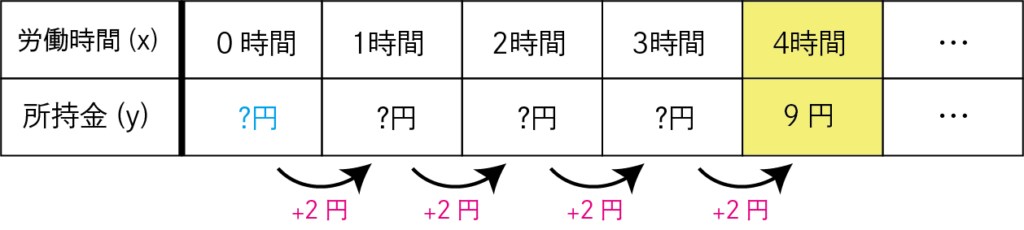
表を見ると「切片」が逆算できることが分かります。
これは「2点の座標」から「切片」を求めた時と同じ考え方です。
4時間労働で?円+8円=9円になっています。
つまり、もとのお金は1円となり。
「変化の割合」が2で、「切片」が1でしたので、\(y=2x+1\)と書けます。
3.「切片」と「1点の座標」で求める
「変化の割合」と「1点の座標」から直線の式を求めるとは、一般的に以下のような問題を出されたときです。
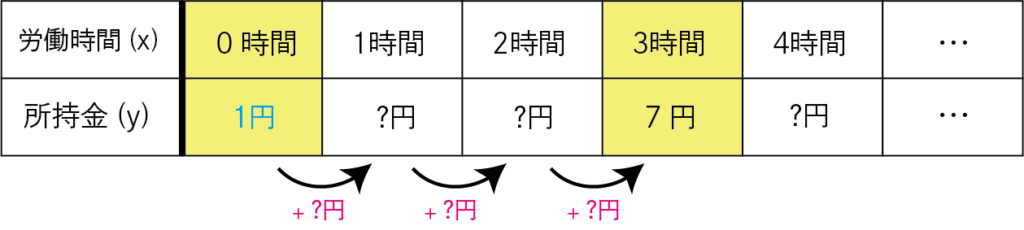
- 切片が1でx=3のとき、y=7の直線の式を求めよ。
- 切片が1で(3,7)を通る直線の式を求めよ。
この問題を表に直すと、
「切片」と〈3時間のとき7円〉が分かっている状態です。
「切片」はわかっているので「変化の割合」だけ求めればいいわけです。
「切片」の座標が分かったので、「2点の座標」が分かっているのと同じです。
「2点の座標」が分かると「変化の割合」を求めることができます。
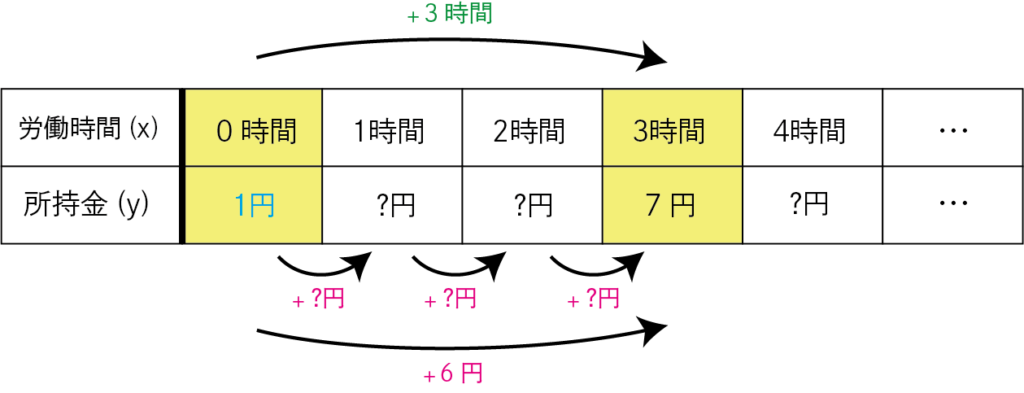
3時間で6円増加しているので、1時間で2円増加と考えられます。
「変化の割合」は2となります。
「変化の割合」が2で、「切片」が1でしたので、\(y=2x+1\)と書けます
まとめ
今回は計算をほとんど使わずに、直線の式\(y=ax+b\)の求め方を解説しました。
数字だけで抽象的に考えるよりも分かりやすかったのではないでしょうか?
「変化の割合」と「切片」と「点の座標」です。
直線の式\(y=ax+b\)のキーワードはこの3つ。
- 「2点の座標」で求める
- 「変化の割合」と「1点の座標」で求める
- 「切片」と「1点の座標」で求める
直線の式\(y=ax+b\)の求め方はこの3種類。
ということだけでも覚えておいてください。


コメント