【図解】一次関数を分かりやすく解説！

一次関数いちじかんすうは中学校の数学のなかでも苦手意識を持ちやすい単元だと思います。
この記事では数学が苦手な人のために小難しい計算はしません。

計算については別の記事で解説します。

まずは一次関数とはどういうものなのか、
簡潔で直感的に理解できるように解説してきたいと思います。

一次関数いちじかんすうの全体像を知る

一次関数とは、とても簡単にいうと
「〇〇のたびに、△△が一定で変化する出来事」です。

例えば、

時給1000円のアルバイト
労働時間が1時間増えるたびに、所持金が1000円ずつ増える。

100円のりんごを何個か買う時
1個買うたびに、所持金が100円ずつ減る。

時速40kmで走る車①
1時間走るたびに、走行距離が40kmずつ増える。

時速40kmで走る車②
1時間走るたびに、目的地までの距離が40kmずつ減る。

このような「〇〇のたびに、△△が一定で変化する出来事」を一次関数では扱っています。

こういう出来事は他にもいっぱいありますよね？
実はそこまで難しい現象を扱っているわけではないのです。

ちなみに、中１で習う「比例」も一次関数の仲間です。

「変化へんかの割合わりあい」と「切片せっぺん」

一次関数では「変化の割合」と「切片」がとても大事になります。
この二つが分かったら問題がほぼ解けたと言っていいくらいに大事です。

「変化の割合」も「切片」も表を使うと理解しやすくなります。

変化の割合

たとえば、時給2円のアルバイトを想像してみてください。

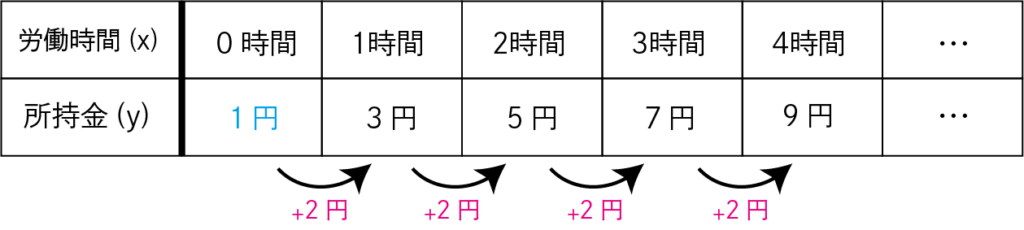
この表は「労働時間が1時間増えるたびに、所持金が2円ずつ増える」ことを表しています。

赤字の部分が「変化の割合」です。
つまりこの場合、「変化の割合」は2となります。

このような一定の変化量を「変化の割合」と呼んでいます。

切片

また表を見てください。

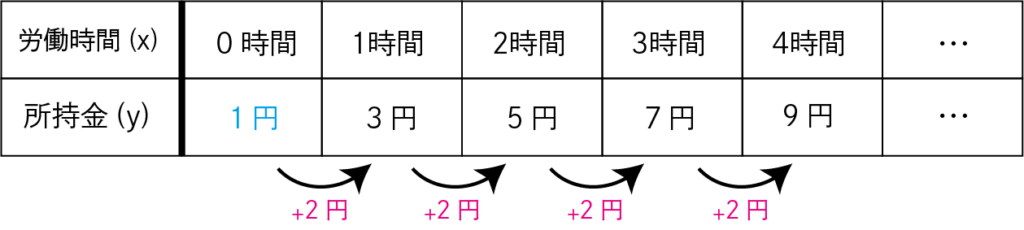
0時間の下の青字の部分が「切片」です。
この場合、「切片」は1となります。

簡単にいうと、0の地点の基準となる数値が「切片」ということです。

一次関数の式(直線の式)　 \(y=ax+b\)

一次関数の式(直線の式)を作る

一次関数は \(y=ax+b\) の式で表すことができます。
aが「変化の割合」、bが「切片」を表しています。
この一次関数の式は直線の式とも呼ばれたりします。

時給2円のアルバイトの表をもう一度見てみましょう。

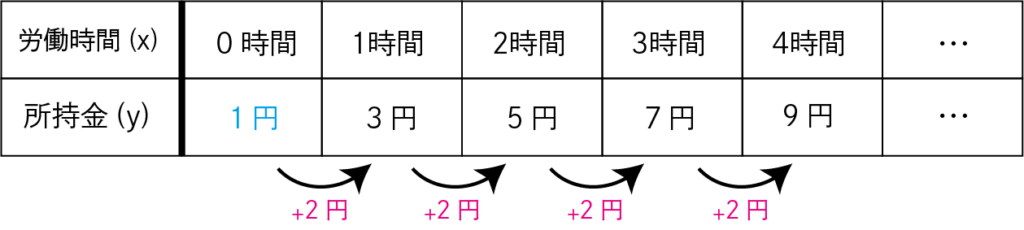
先ほど「変化の割合」が2、「切片」が1と分かりましたよね。

\(y=ax+b\) の
\(a\) に「変化の割合」の2、\(b\) に「切片」の1を代入すると、
この表は \(y=2x+1\) と書き表すことができます。

文字の式になると難しく見えるかもしれませんが、
それぞれに「変化の割合」と「切片」の数値をそのまま入れるだけです。

やってることはとてもシンプルなのです。

式から「変化の割合」と「切片」を読み解く

先ほどは表から\(y=ax+b\)の式を作りましたが、その逆も可能です。

例えば、\(y=5x+3\)という式があったとしたら、
変化の割合が5、切片が3と答えることができます。

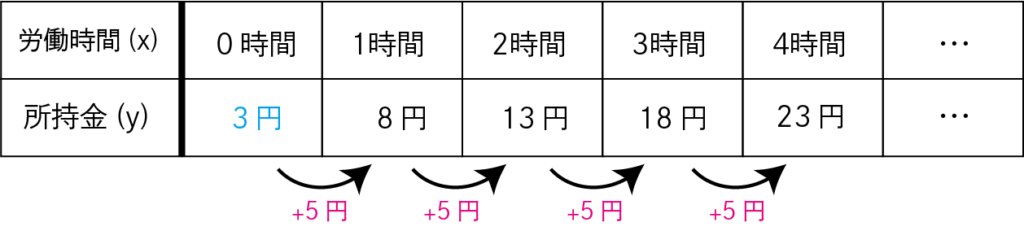
そうすると、このような変化をする出来事だと想像できます。

一次関数の式の使い方

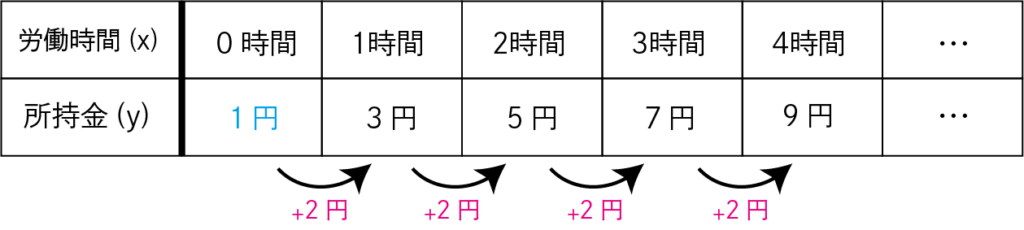
この表を見たとき、「労働時間3時間のときの所持金がいくらか？」というのは表を見れば分かりますよね。

「グラフ」と「表」と「式」の関係

一次関数は、式で書き表せるだけでなく、グラフに直線としても表現することができます。
さきほどの時給2円のアルバイトの表と式をグラフにしてみましょう。

「表」から「グラフ」へ

まずは、表をグラフに書き直してみましょう。
労働時間をx、所持金をyとしたときに下のようなグラフが書けます。

0時間と1円、1時間と3円のような、上下の数字の組み合わせが座標として書き表せます。

x時間とy円→（x,y）
0時間と1円→（0,1）
1時間と3円→（1,3）
2時間と5円→（2,5）
3時間と7円→（3,7）

それらを座標の点を結ぶと直線となります。

「式」から「グラフ」へ

\(y=ax+b\)の式もグラフ上の直線として表現することができます。

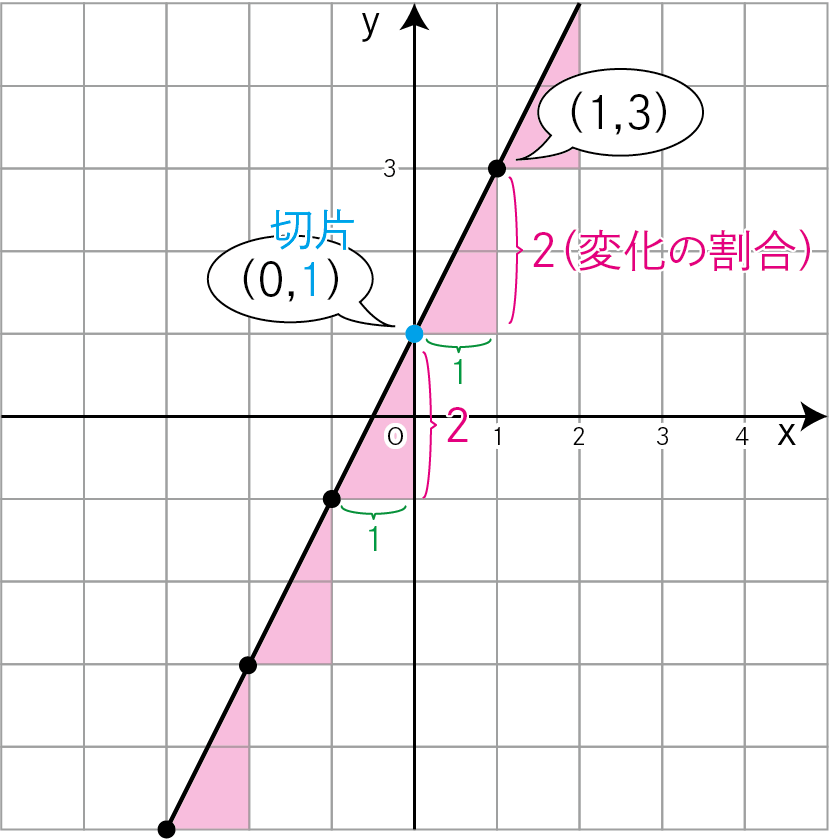
先ほどの時給2円のアルバイトの表は \(y=2x+1\) と表現できましたよね。

「変化の割合」は赤字の2の部分、
「切片」はy軸上の1の部分となります。

底辺１の赤い三角形の高さが「変化の割合」
y軸上にできた点が「切片」

まずはこのように覚えておくといいと思います。

まとめ

一次関数とはどんなものか、できるだけ具体的な例を使ってかなり簡潔に解説してみました。

変化の割合、切片、\(y=ax+b\)、グラフはどの一次関数の問題でも大事です。
しっかり覚えましょう。

理屈を冷静に見ていくとやっていることはそこまで難しいことはしていません。
あまり苦手意識を持たずに取り組んでみてほしいです。