この記事では正負の数の乗法と除法を解説します。
乗法と除法とは、掛け算と割り算のことです。
まずは掛け算から解説していきます。
さて、正負の数の掛け算では以下のような計算をします。
- \((+1)\times(+2)=+2\)
- \((+1)\times(-2)=-2\)
- \((-1)\times(+2)=-2\)
- \((-1)\times(-2)=+2\)
さて、ここで疑問に思うのは、
-2倍ってなんだ?
ということだと思います。
乗法・掛け算とは
掛け算について改めて考えてみましょう。
たとえば、\((+1) \times (+2) \) は
「1を2回足す」と考えることができます。
「1を2回足す」と+2になります。
\((+3) \times (+4)\) は
「3を4回足す」ので+12です。
では、\((+1) \times (-2) \) は
「1を2回引く」と考えてみてはどうでしょうか?
すると答えは-2になります。
このように乗法(掛け算)は
加法(足し算)と減法(引き算)の組み合わせとして
考えることができます。
乗法の計算イメージ
\((+1) \times (+2) \) を「1を2回足す」と読めば、
\(0+(+1)+(+1)=+2\) という計算ができます。
同様に、
\((+1)\times(-2)=-2\) は「1を2回引く」で
\(0-(+1)-(+1)=-2\)
\((-1)\times(+2)=-2\) は \(0+(-1)+(-1)=-2\)
\((-1)\times(-2)=+2\) は \(0-(-1)-(-1)=+2\)
と書くことができます。
それぞれのイメージが以下のようになります。
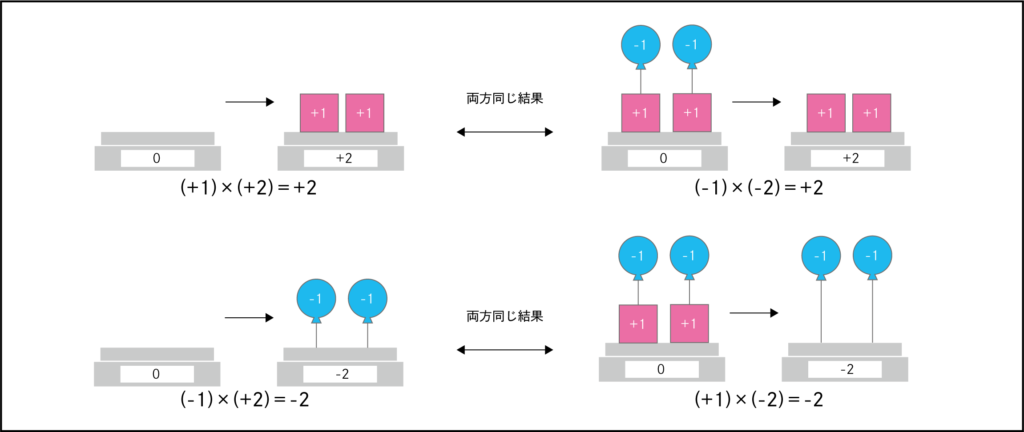
\((+1)\times(-2)=-2\) (1を2回引く)と
\((-1)\times(-2)=+2\)(-1を2回引く)は、
すこしイメージしづらいので、
「風船」と「重り」の組み合わせの0からそれぞれを引きました。
0はいくつ足しても0なので、こういう考え方ができます。
また、乗法は加法と減法の組み合わせなので、
-(-1)を+1としたり、-(+1)を+(-1)としたり書き換えることができます。
よって、
\((+1) \times (+2) \) と\((-1)\times(-2)\)が同じ結果、
\((+1)\times(-2)\)と\((-1)\times(+2)\)が同じ結果になります。
乗法の計算方法
掛け算の仕組みやイメージを解説してきました。
ただ実際に計算はもっとシンプルです。
数の部分は普通に掛け算の計算をし、
マイナス×マイナスのように、
マイナスの個数が偶数なら答えの符号をプラスにします。
マイナスが0の時もプラスです。
プラス×マイナスのように
マイナスの個数が奇数なら答えの符号をマイナスにします。
(偶数というのは2の倍数と考えましょう。0,2,4,6,8,10…..)
実際に計算を見てみましょう。
- \((+1)\times(+2)=+2\) マイナスが0個、偶数なのでプラス
- \((+1)\times(-2)=-2\) マイナスが1個、奇数なのでマイナス
- \((-1)\times(+2)=-2\) マイナスが1個、奇数なのでマイナス
- \((-1)\times(-2)=+2\) マイナスが2個、偶数なのでプラス
- \((+1)\times(+2)\times(+2)=+4\) マイナスが0個、偶数なのでプラス
- \((+1)\times(-2)\times(+2)=-4\) マイナスが1個、奇数なのでマイナス
- \((-1)\times(+2)\times(-2)=+4\) マイナスが2個、偶数なのでプラス
- \((-1)\times(-2)\times(-2)=-4\) マイナスが3個、奇数なのでマイナス
符号の数を間違えると、
計算結果が変わってしまうので気を付けましょう。
除法・割り算とは
割り算について改めて考えてみましょう。
掛け算の考え方を応用してみます。
たとえば、((+4) \div (+2) ) は
単純に4の半分と考えられますが、
「4の2分の1を足す」とも考えることができます。
「4の2分の1を足す」と+2になります。
\((+6) \times (+3)\) は
「6の3分の1を足す」ので+2です。
逆に\((+4) \div (-2) \)は
「4の2分の1を引く」と考えれば
答えは-2になります。
除法の計算方法
正負の数の除法は一般的な割り算のように計算が可能です。
- \((+4)\div(+2)=+2\)
- \((+4)\div(-2)=-2\)
- \((-4)\div(+2)=-2\)
- \((-4)\div(-2)=+2\)
乗法でやったように、マイナスの符号の数で
答えのプラスとマイナスが変化します。
マイナスの個数が
偶数ならプラス、奇数ならマイナスのような感じです。
除法を乗法で計算する
割り算は逆数を使うことで掛け算で計算することができます。
正負の数でも同様のことができます。
- \((+4)\div(+2)=+2\) → \((+4)\times(+\frac{1}{2})=+2\)
- \((+4)\div(-2)=-2\) → \((+4)\times(-\frac{1}{2})=-2\)
- \((-4)\div(+2)=-2\) → \((-4)\times(+\frac{1}{2})=-2\)
- \((-4)\div(-2)=+2\) → \((-4)\times(-\frac{1}{2})=+2\)
あとは計算の規則は先ほどの掛け算のやり方と同じです。
マイナス符号の数で答えの符号が決まります。
乗法と除法の混じった計算
掛け算と割り算の混ざった計算のコツを解説します。
コツは「全部掛け算に直す」です。
\((+3)\times(+8)\div(+2)\)なら、
\((+3)\times(+8)\times(+\frac{1}{2})=+12\)
のように計算しましょう。コツはこれだけです。
計算が苦手な人ほど徹底してやった方がいいです。
むしろ計算の苦手な人ほど省こうとします。
計算ミスには気を付けましょう。
まとめ
正負の数の乗法と除法は計算こそシンプルですが、
計算の仕組みがわからないと、少し難しく感じることでしょう。
この記事で少しでも、計算のイメージを持ってもらえたら嬉しいです。
「マイナス符号の数で答えの符号が変わる」ことはしっかり意識して、
計算ミスをしないように注意しましょう。


コメント