【図解】正負の数 を分かりやすく解説！

正負の数ではマイナス、つまり0より小さい数が出てきます。

たとえば、-1個のリンゴを想像してみましょう。
何が思い浮かぶでしょうか？
想像するのは少し難しいかもしれませんね。
では、０より小さいとはどういうことなのでしょう。

まず結論からいうと、
リンゴの個数が0より少なくなることはありません。
ですが、-1個のリンゴを存在させることは可能です。

矛盾しているように聞こえますが、
考え方によっては両方が成り立ってしまいます。

さて、その考え方とはどんなものなのでしょうか。
この記事では正負の数の考え方について解説していきます。

正の数、負の数

0より大きい数を正の数、0より小さい数を負の数と言います。

正の数を表すときには、＋（プラス）をつけ、
負の数を表すときには、-(マイナス)をつけます。

この+や-の記号を「符号」と言い、それぞれ正の符号、負の符号と呼びます。

正の数ならば、+1、+15、+3.5
負の数ならば、-1、-15、-3.5のように書きます。

また、一般的には数直線を使って、これらの数字を表現します。
ちなみに、数字部分のことを絶対値と呼びます。

0の考え方

正負の数で重要なこと、それは「0の考え方」です。

この0の考え方があるおかげで、
0より小さい数というものを表現できるようになります。

小学校までの計算では何もない状態を0と表すことが多かったかと思います。
しかし、その考え方だけでは、正負の数を理解できません。

正負の数では、0は何もない状態以外のことも表します。

基準を表す0

ある状態を基準として、それを0とするものです。
その基準よりどれだけ大きいか小さいかを、プラスとマイナスを使って表現します。

温度計が良い例でしょう。
温度計の0は一番低い温度ではありませんよね。

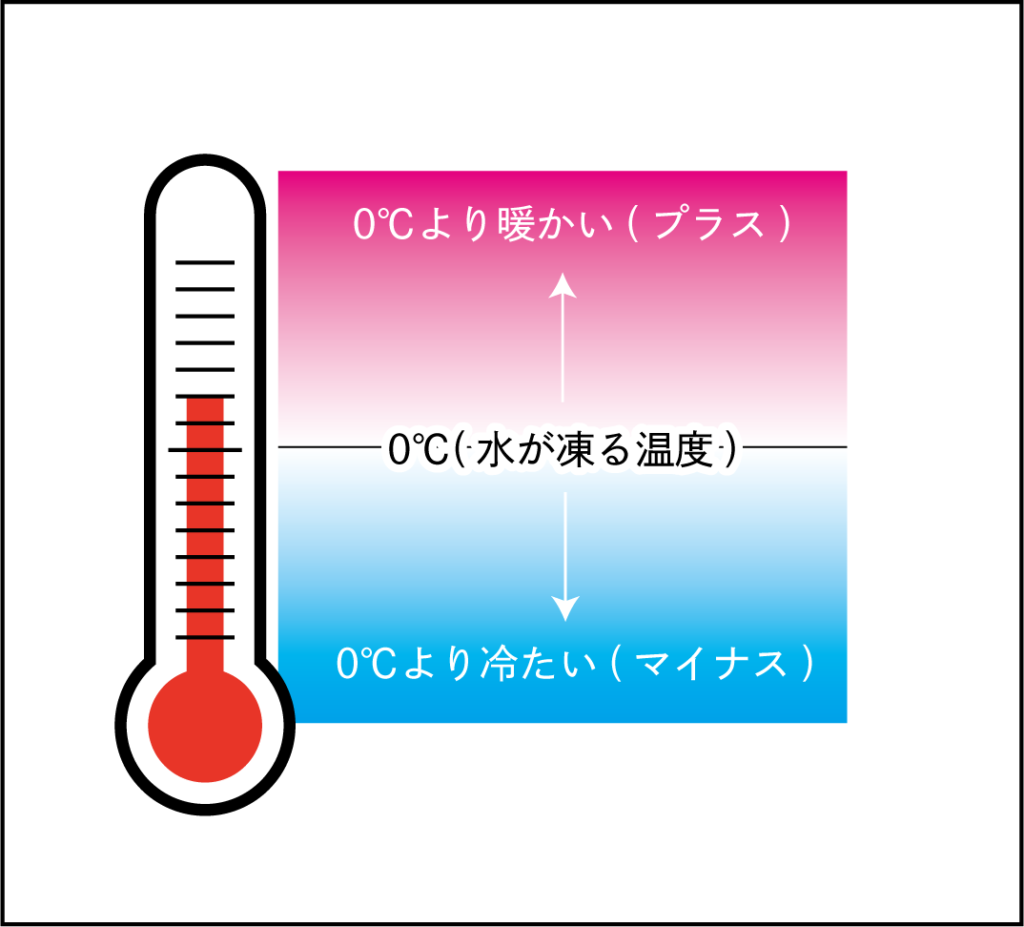
水が凍る温度を基準0℃として、それより高いか低いかで温度を表現しています。

基準から10℃高ければ+10℃
基準より10℃低ければ-10℃

上記とは違う基準の温度表記もあります。
主に海外で使われ、華氏(℉)と呼ばれています。
私たちが日常的に使う温度表記は摂氏(℃)と言います。

温度表記の他にも地球儀の経度、緯度などもそうですよね。
経度0度はイギリスのロンドン、緯度0度は赤道を基準にしています。

0を基準として使うことで、
場所や状態など、様々な出来事を簡単に表すことができます。

数量を表す0

次に、1-1=0を考えてみましょう。

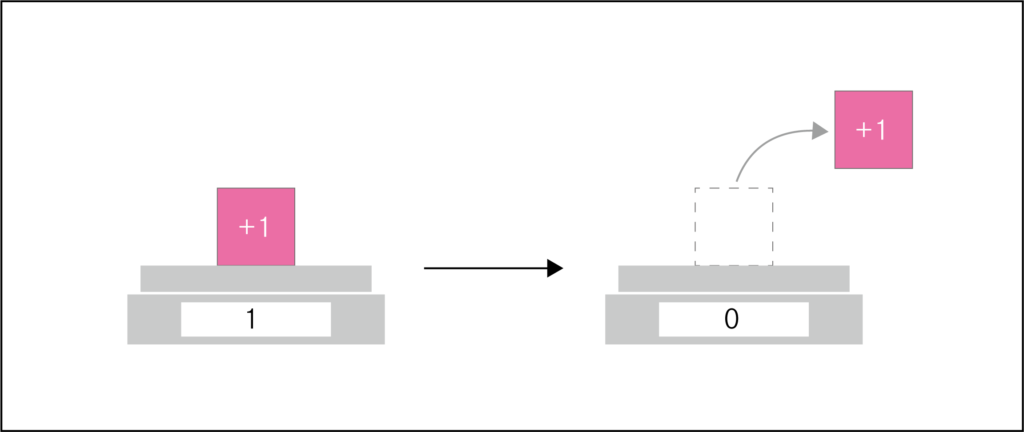
何もない状態を0とする考え方ですね。
物を数えるときはこのようにするのが一般的です。

しかし、正負の数では別の考え方も扱います。
下の図をみてください。

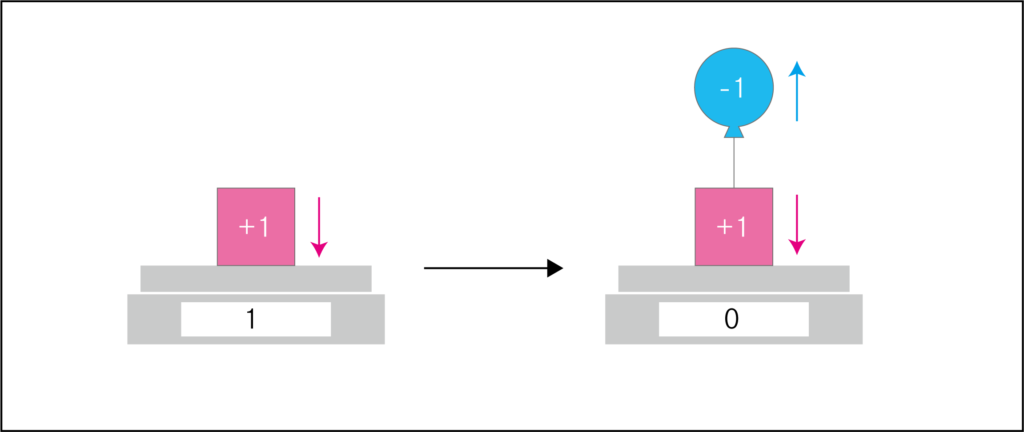
別の考え方とは、重さが打ち消されるときです。
青い風船が重りを上に引っ張って、重さを無くしています。

物が無くなってないのに結果が0になっています。

これも1-1=0と考えることができます。

０より小さい数

さて、先ほどの0の考え方を踏まえて、
0より小さい数について考えてみましょう。

状態を表す

先ほど温度計の話をしました。

ある状態を基準0として、
それより大きければプラス、小さければマイナスと表記します。

-1個のリンゴ　その１

ここで-１個のリンゴについて考えてみましょう。
りんごの個数が０個よりも少なくなることは現実的にはあり得ません。

しかし、例えば、10個のリンゴを持っていることを基準としたら、
リンゴ9個の時を-1個と表現してもいいのです。

-１個のリンゴとは、基準より1個少ない状態と捉えることができます

注意して欲しいのは、
あくまで、表現できるだけであって、
適切な状況で使わないと意味が分からないことです。

変化量を表す

正負の数の計算では、
増えることをプラス、減ることをマイナスの変化量として扱います。

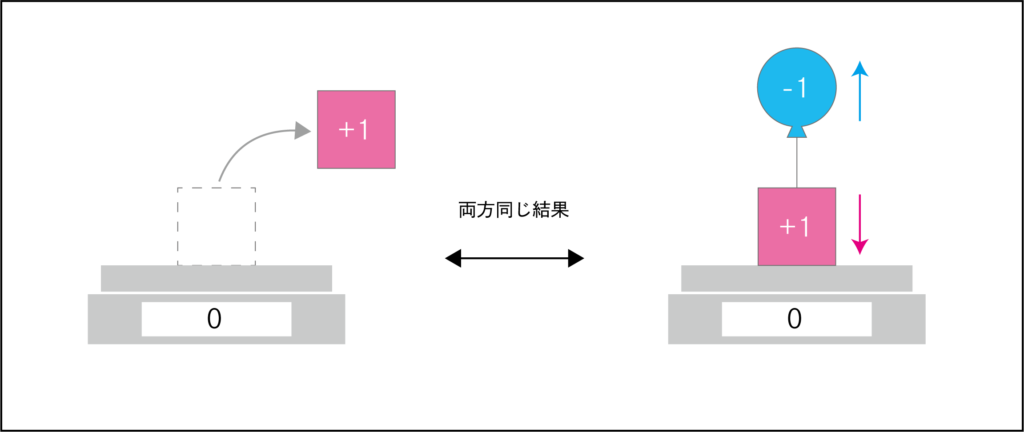
図にあるように、方法は違っても、同じ結果が得られます。
このようなとき、重りをプラス、風船をマイナスと表現することができます。

プラスとは逆向きの要素が0より小さいということなのです。

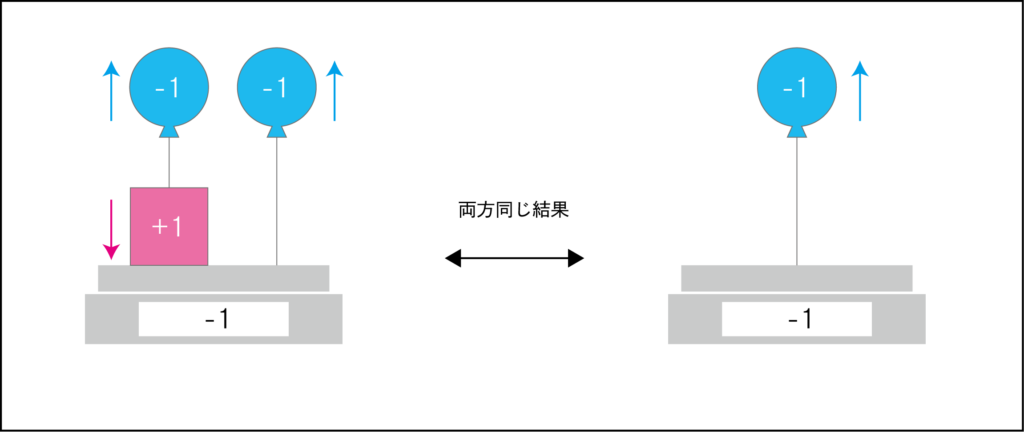
また、このマイナスがプラスよりも多い状態もマイナスと表現します。
図の場合、重りより風船が一つ多いので、-1となります。
(実際の計量器ではマイナスの値は出ません)

-1個のリンゴ　その２

ここでも-1個のリンゴを考えてみましょう。

リンゴが増えることをプラスとするなら、
リンゴが減ってしまうことをマイナスと考えることができます。

例えば、2個しかリンゴを持っていないのに、
3人にリンゴを一個ずつあげなければいけなくなりました。

この時、リンゴをもらう人を-1個のリンゴと表現することができます。
また、2-3=-1という計算はリンゴをもらえない人が1人いますよ、と解釈できます。

-1個のリンゴとは、
あくまで表現であって、実在するというわけではありません。

正負の数の計算

正負の数の考え方は非常にシンプルです。

プラスとマイナス、どちらがどれだけ多いか

です。

二つの要素で計算する

お互いが打ち消し合うような要素、正反対の性質、
それらを一緒に計算するのが正負の数の計算です。

• 重りを足せば、重くなる。
• 重りを引けば、軽くなる。
• 風船を足せば、軽くなる。
• 風船を引けば、重くなる。

そして、最終的にどちらがどれだけ多いのか、を計算します。
やることはシンプルです。

重りと風船以外にも、
「お金が増える、お金が減る」、「西に進む、東に進む」
のような、何かの増減で考えてみても良いと思います。

結果を重視する

重りを引けば、軽くなる。
風船を足せば、軽くなる。

違う動作ですが、同じ結果が得られます。
これらは計算上区別しないで書くことができます。

どちらも1-1=0と書けます。(他の書き方もあります)

なので、計算ルールさえ分かれば、
図のようなことを考えなくても計算できるようになります。

まとめ

この正負の数の計算は、「正反対の要素を一緒に扱う」
このことが分かっていることが大切です。

途中-1個のリンゴの話が出たと思います。
あれらの話は少し屁理屈のように聞こえるかもしれません。

しかし、数字で表現できるということがとても大事なのです。

表現できるというのは、自分以外の人や物と協力するために不可欠です。
表現によって、協力し、それによって私たちの生活は豊かになってきました。
ほんの些細なことに思えるかもしれませんが、
その積み重ねが今の私たちの生活を作っています。

数学をただの計算するだけの学問と思うと楽しくないかもしれません。
「数字で表現する」、それが数学の面白いところでもあります。